
Главные компоненты и факторный анализ
Основная цель
Главными целями факторного анализа являются: (1) сокращение числа переменных (редукция данных) и (2) определение структуры взаимосвязей между переменными, т.е. классификация переменных. Поэтому факторный анализ используется или как метод сокращения данных или как метод классификации. Ниже описываются принципы факторного анализа и способы его применения для достижения этих двух целей. Предполагается, что вы знакомы с логикой статистических выводов в объеме, содержащемся в разделе Элементарные понятия статистики. Предполагается также, что вы знакомы с понятиями дисперсии и корреляции (см. например, раздел Основные статистики и таблицы).
Существует множество прекрасных книг по факторному анализу. Практические примеры и советы по применению можно, например, найти в книге Стивенса (Stevens, 1986); более подробное описание приводят Кули и Лонес (Cooley, Lohnes, 1971); Харман (Harman, 1976); Ким и Мюллер (Kim, Mueller, 1978a, 1978b); Лоули и Максвелл (Lawley, Maxwell, 1971); Линдеман, Меренда и Голд (Lindeman, Merenda, Gold, 1980); Моррисон (Morrison, 1967) и Мулэйк (Mulaik, 1972). Интерпретация вторичных факторов в иерархическом факторном анализе, как альтернатива традиционному вращению факторов, дана Верри (Wherry, 1984).
Подтверждающий факторный анализ. Моделирование структурными уравнениями (SEPATH) позволяет проверять частные гипотезы о факторной структуре для множества переменных (подтверждающий факторный анализ) в одной или нескольких выборках (например, вы сможете сравнить факторные структуры разных выборок (опытов)).
Анализ соответствий. Анализ соответствий - это описательные/разведочные методы, предназначенные для анализа двух- и многовходовых таблиц, содержащих некоторые взаимосвязи между строками и столбцами. Результаты этого анализа дают информацию, похожую на ту, которую предоставляет факторный анализ, и позволяют изучить структуру категориальных переменных, входящих в таблицу. За более полной информацией об этих методах обратитесь к описанию Анализа соответствий.
| В начало |
Факторный анализ как метод редукции данных
Предположим, что вы проводите (до некоторой степени "глупое") исследование, в котором измеряете рост ста людей в дюймах и сантиметрах. Таким образом, у вас имеются две переменные. Если далее вы захотите исследовать, например, влияние различных пищевых добавок на рост, будете ли вы продолжать использовать обе переменные? Вероятно, нет, т.к. рост является одной характеристикой человека, независимо от того, в каких единицах он измеряется.
Теперь предположим, вы хотите измерить удовлетворенность людей жизнью, для чего составляете вопросник с различными пунктами; среди других вопросов задаете следующие: удовлетворены ли люди своим хобби (пункт 1) и как интенсивно они им занимаются (пункт 2). Результаты преобразуются так, что средние ответы (например, для удовлетворенности) соответствуют значению 100, в то время как ниже и выше средних ответов расположены меньшие и большие значения, соответственно. Две переменные (ответы на два разных пункта) коррелированы между собой. (Если вы не знакомы с понятием коэффициента корреляции, рекомендуем обратиться к разделу Основные статистики и таблицы - Корреляции). Из высокой коррелированности двух этих переменных можно сделать вывод об избыточности двух пунктов опросника.
Объединение двух переменных в один фактор. Зависимость между переменными можно обнаружить с помощью диаграммы рассеяния. Полученная путем подгонки линия регрессии дает графическое представление зависимости. Если определить новую переменную на основе линии регрессии, изображенной на этой диаграмме, то такая переменная будет включить в себя наиболее существенные черты обеих переменных. Итак, фактически, вы сократили число переменных и заменили две одной. Отметим, что новый фактор (переменная) в действительности является линейной комбинацией двух исходных переменных.
Анализ главных компонент. Пример, в котором две коррелированные переменные объединены в один фактор, показывает главную идею факторного анализа или, более точно, анализа главных компонент (это различие будет обсуждаться позднее). Если пример с двумя переменными распространить на большее число переменных, то вычисления становятся сложнее, однако основной принцип представления двух или более зависимых переменных одним фактором остается в силе.
Выделение главных компонент. В основном процедура выделения главных компонент подобна вращению, максимизирующему дисперсию (варимакс) исходного пространства переменных. Например, на диаграмме рассеяния вы можете рассматривать линию регрессии как ось X, повернув ее так, что она совпадает с прямой регрессии. Этот тип вращения называется вращением, максимизирующим дисперсию, так как критерий (цель) вращения заключается в максимизации дисперсии (изменчивости) "новой" переменной (фактора) и минимизации разброса вокруг нее (см. Стратегии вращения).
Обобщение на случай многих переменных. В том случае, когда имеются более двух переменных, можно считать, что они определяют трехмерное "пространство" точно так же, как две переменные определяют плоскость. Если вы имеете три переменные, то можете построить 3М диаграмму рассеяния.

Для случая более трех переменных, становится невозможным представить точки на диаграмме рассеяния, однако логика вращения осей с целью максимизации дисперсии нового фактора остается прежней.
Несколько ортогональных факторов. После того, как вы нашли линию, для которой дисперсия максимальна, вокруг нее остается некоторый разброс данных. И процедуру естественно повторить. В анализе главных компонент именно так и делается: после того, как первый фактор выделен, то есть, после того, как первая линия проведена, определяется следующая линия, максимизирующая остаточную вариацию (разброс данных вокруг первой прямой), и т.д. Таким образом, факторы последовательно выделяются один за другим. Так как каждый последующий фактор определяется так, чтобы максимизировать изменчивость, оставшуюся от предыдущих, то факторы оказываются независимыми друг от друга. Другими словами, некоррелированными или ортогональными.
Сколько факторов следует выделять? Напомним, что анализ главных компонент является методом сокращения или редукции данных, т.е. методом сокращения числа переменных. Возникает естественный вопрос: сколько факторов следует выделять? Отметим, что в процессе последовательного выделения факторов они включают в себя все меньше и меньше изменчивости. Решение о том, когда следует остановить процедуру выделения факторов, главным образом зависит от точки зрения на то, что считать малой "случайной" изменчивостью. Это решение достаточно произвольно, однако имеются некоторые рекомендации, позволяющие рационально выбрать число факторов, как показано в Обзоре результатов анализа главных компонент, см. раздел Собственные значения и задача о числе факторов.
Обзор результатов анализа главных компонент. Посмотрим теперь на некоторые стандартные результаты анализа главных компонент. При повторных итерациях вы выделяете факторы с все меньшей и меньшей дисперсией. Для простоты изложения считаем, что обычно работа начинается с матрицы, в которой дисперсии всех переменных равны 1.0. Поэтому общая дисперсия равна числу переменных. Например, если вы имеете 10 переменных, каждая из которых имеет дисперсию 1, то наибольшая изменчивость, которая потенциально может быть выделена, равна 10 раз по 1. Предположим, что при изучении степени удовлетворенности жизнью вы включили 10 пунктов для измерения различных аспектов удовлетворенности домашней жизнью и работой. Дисперсия, объясненная последовательными факторами, представлена в следующей таблице:
| STATISTICA ФАКТОРНЫЙ АНАЛИЗ |
Собственные
значения (factor.sta) Выделение: Главные компоненты |
|||
|---|---|---|---|---|
| Значение |
Собственные значения |
% общей дисперсии |
Кумулят. соб. знач. |
Кумулят. % |
| 1 2 3 4 5 6 7 8 9 10 |
6.118369 1.800682 .472888 .407996 .317222 .293300 .195808 .170431 .137970 .085334 |
61.18369 18.00682 4.72888 4.07996 3.17222 2.93300 1.95808 1.70431 1.37970 .85334 |
6.11837 7.91905 8.39194 8.79993 9.11716 9.41046 9.60626 9.77670 9.91467 10.00000 |
61.1837 79.1905 83.9194 87.9993 91.1716 94.1046 96.0626 97.7670 99.1467 100.0000 |
Собственные значения
Во втором столбце (Собственные значения) таблицы
результатов вы можете найти дисперсию нового,
только что выделенного фактора. В третьем
столбце для каждого фактора приводится процент
от общей дисперсии (в данном примере она равна 10)
для каждого фактора. Как можно видеть, первый
фактор (значение 1) объясняет 61 процент общей
дисперсии, фактор 2 (значение 2) - 18 процентов, и т.д.
Четвертый столбец содержит накопленную или
кумулятивную дисперсию. Дисперсии, выделяемые
факторами, названы собственными значениями.
Это название происходит из использованного
способа вычисления.
Собственные значения и задача о числе
факторов
Как только получена информация о том, сколько
дисперсии выделил каждый фактор, вы можете
возвратиться к вопросу о том, сколько факторов
следует оставить. Как говорилось выше, по своей
природе это решение произвольно. Однако имеются
некоторые общеупотребительные рекомендации, и
на практике следование им дает наилучшие
результаты.
Критерий Кайзера. Сначала вы можете отобрать только факторы, с собственными значениями, большими 1. По существу, это означает, что если фактор не выделяет дисперсию, эквивалентную, по крайней мере, дисперсии одной переменной, то он опускается. Этот критерий предложен Кайзером (Kaiser, 1960), и является, вероятно, наиболее широко используемым. В приведенном выше примере на основе этого критерия вам следует сохранить только 2 фактора (две главные компоненты).
Критерий каменистой осыпи. Критерий каменистой осыпи является графическим методом, впервые предложенным Кэттелем (Cattell, 1966). Вы можете изобразить собственные значения, представленные в таблице ранее, в виде простого графика.
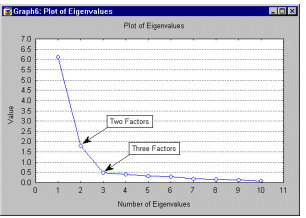
Кэттель предложил найти такое место на графике, где убывание собственных значений слева направо максимально замедляется. Предполагается, что справа от этой точки находится только "факториальная осыпь" - "осыпь" является геологическим термином, обозначающим обломки горных пород, скапливающиеся в нижней части скалистого склона. В соответствии с этим критерием можно оставить в этом примере 2 или 3 фактора.
Какой критерий следует использовать. Оба критерия были изучены подробно Брауном (Browne, 1968), Кэттелем и Джасперсом (Cattell, Jaspers, 1967), Хакстианом, Рожерсом и Кэттелем (Hakstian, Rogers, Cattell, 1982), Линном (Linn, 1968), Тюкером, Купманом и Линном (Tucker, Koopman, Linn, 1969). Теоретически, можно вычислить их характеристики путем генерации случайных данных для конкретного числа факторов. Тогда можно увидеть, обнаружено с помощью используемого критерия достаточно точное число существенных факторов или нет. С использованием этого общего метода первый критерий (критерий Кайзера) иногда сохраняет слишком много факторов, в то время как второй критерий (критерий каменистой осыпи) иногда сохраняет слишком мало факторов; однако оба критерия вполне хороши при нормальных условиях, когда имеется относительно небольшое число факторов и много переменных. На практике возникает важный дополнительный вопрос, а именно: когда полученное решение может быть содержательно интерпретировано. Поэтому обычно исследуется несколько решений с большим или меньшим числом факторов, и затем выбирается одно наиболее "осмысленное". Этот вопрос далее будет рассматриваться в рамках вращений факторов.
Анализ главных факторов
Прежде, чем продолжить рассмотрение различных
аспектов вывода анализа главных компонент,
введем анализ главных факторов. Вернемся к
примеру вопросника об удовлетворенности жизнью,
чтобы сформулировать другую "мыслимую
модель". Вы можете представить себе, что ответы
субъектов зависят от двух компонент. Сначала
выбираем некоторые подходящие общие факторы,
такие как, например, "удовлетворение своим
хобби", рассмотренные ранее. Каждый пункт
измеряет некоторую часть этого общего аспекта
удовлетворения. Кроме того, каждый пункт
включает уникальный аспект удовлетворения, не
характерный для любого другого пункта.
Общности. Если эта модель правильна, то вы не можете ожидать, что факторы будут содержать всю дисперсию в переменных; они будут содержать только ту часть, которая принадлежит общим факторам и распределена по нескольким переменным. На языке факторного анализа доля дисперсии отдельной переменной, принадлежащая общим факторам (и разделяемая с другими переменными) называется общностью. Поэтому дополнительной работой, стоящей перед исследователем при применении этой модели, является оценка общностей для каждой переменной, т.е. доли дисперсии, которая является общей для всех пунктов. Доля дисперсии, за которую отвечает каждый пункт, равна тогда суммарной дисперсии, соответствующей всем переменным, минус общность. С общей точки зрения в качестве оценки общности следует использовать множественный коэффициент корреляции выбранной переменной со всеми другими (для получения сведений о теории множественной регрессии сошлемся на раздел Множественная регрессия). Некоторые авторы предлагают различные итеративные "улучшения после решения" начальной оценки общности, полученной с использованием множественной регрессии; например, так называемый метод MINRES (метод минимальных факторных остатков; Харман и Джоунс (Harman, Jones, 1966)), который производит испытание различных модификаций факторных нагрузок с целью минимизации остаточных (необъясненных) сумм квадратов.
Главные факторы в сравнении с главными компонентами. Главные факторы в сравнении с главными компонентами. Основное различие двух моделей факторного анализа состоит в том, что в анализе главных компонент предполагается, что должна быть использована вся изменчивость переменных, тогда как в анализе главных факторов вы используете только изменчивость переменной, общую и для других переменных. Подробное обсуждение всех "за" и "против" каждого подхода находится за пределами данного введения. В большинстве случаев эти два метода приводят к весьма близким результатам. Однако анализ главных компонент часто более предпочтителен как метод сокращения данных, в то время как анализ главных факторов лучше применять с целью определения структуры данных (см. следующий раздел).
| В начало |
Факторный анализ как метод классификации
Возвратимся к интерпретации результатов факторного анализа. Термин факторный анализ теперь будет включать как анализ главных компонент, так и анализ главных факторов. Предполагается, что вы находитесь в той точке анализа, когда в целом знаете, сколько факторов следует выделить. Вы можете захотеть узнать значимость факторов, то есть, можно ли интерпретировать их разумным образом и как это сделать. Чтобы проиллюстрировать, каким образом это может быть сделано, производятся действия "в обратном порядке", то есть, начинают с некоторой осмысленной структуры, а затем смотрят, как она отражается на результатах. Вернемся к примеру об удовлетворенности; ниже приведена корреляционная матрица для переменных, относящихся к удовлетворенности на работе и дома.
| STATISTICA ФАКТОРНЫЙ АНАЛИЗ |
Корреляции
(factor.sta) Построчное удаление ПД n=100 |
|||||
|---|---|---|---|---|---|---|
| Переменная | РАБОТА_1 | РАБОТА_2 | РАБОТА_3 | ДОМ_1 | ДОМ_2 | ДОМ_3 |
| РАБОТА_1 РАБОТА_2 РАБОТА_3 ДОМ_1 ДОМ_2 ДОМ_3 |
1.00 .65 .65 .14 .15 .14 |
.65 1.00 .73 .14 .18 .24 |
.65 .73 1.00 .16 .24 .25 |
.14 .14 .16 1.00 .66 .59 |
.15 .18 .24 .66 1.00 .73 |
.14 .24 .25 .59 .73 1.00 |
Переменные, относящиеся к удовлетворенности на
работе, более коррелированы между собой, а
переменные, относящиеся к удовлетворенности
домом, также более коррелированы между собой.
Корреляции между этими двумя типами переменных
(переменные, связанные с удовлетворенностью на
работе, и переменные, связанные с
удовлетворенностью домом) сравнительно малы.
Поэтому кажется правдоподобным, что имеются два
относительно независимых фактора (два типа
факторов), отраженных в корреляционной матрице:
один относится к удовлетворенности на работе, а
другой к удовлетворенности домашней жизнью.
Факторные нагрузки. Теперь проведем анализ главных компонент и рассмотрим решение с двумя факторами. Для этого рассмотрим корреляции между переменными и двумя факторами (или "новыми" переменными), как они были выделены по умолчанию; эти корреляции называются факторными нагрузками.
| STATISTICA ФАКТОРНЫЙ АНАЛИЗ |
Факторные
нагрузки (Нет вращения) Главные компоненты |
|
|---|---|---|
| Переменная | Фактор 1 | Фактор 2 |
| РАБОТА_1 РАБОТА_2 РАБОТА_3 ДОМ_1 ДОМ_2 ДОМ_3 |
.654384 .715256 .741688 .634120 .706267 .707446 |
.564143 .541444 .508212 -.563123 -.572658 -.525602 |
| Общая дисперсия Доля общей дисп. |
2.891313 .481885 |
1.791000 .298500 |
По-видимому, первый фактор более коррелирует с
переменными, чем второй. Это следовало ожидать,
потому что, как было сказано выше, факторы
выделяются последовательно и содержат все
меньше и меньше общей дисперсии.
Вращение факторной структуры. Вы можете изобразить факторные нагрузки в виде диаграммы рассеяния. На этой диаграмме каждая переменная представлена точкой. Можно повернуть оси в любом направлении без изменения относительного положения точек; однако действительные координаты точек, то есть факторные нагрузки, должны, без сомнения, меняться. Если вы построите диаграмму для этого примера, то увидите, что если повернуть оси относительно начала координат на 45 градусов, то можно достичь ясного представления о нагрузках, определяющих переменные: удовлетворенность на работе и дома.
Методы вращения. Существуют различные методы вращения факторов. Целью этих методов является получение понятной (интерпретируемой) матрицы нагрузок, то есть факторов, которые ясно отмечены высокими нагрузками для некоторых переменных и низкими - для других. Эту общую модель иногда называют простой структурой (более формальное определение можно найти в стандартных учебниках). Типичными методами вращения являются стратегии варимакс, квартимакс, и эквимакс.
Идея вращения по методу варимакс была описана выше (см. Выделение главных компонент), и этот метод можно применить успешно и к рассматриваемой задаче. Как и ранее, вы хотите найти вращение, максимизирующее дисперсию по новым осям; другими словами, вы хотите получить матрицу нагрузок на каждый фактор таким образом, чтобы они отличались максимально возможным образом и имелась возможность их простой интерпретации. Ниже приведена таблица нагрузок на повернутые факторы.
| STATISTICA ФАКТОРНЫЙ АНАЛИЗ |
Факторные
нагрузки (Варимакс нормализ.) Выделение: Главные компоненты |
|
|---|---|---|
| Переменная | Фактор 1 | Фактор 2 |
| РАБОТА_1 РАБОТА_2 РАБОТА_3 ДОМ_1 ДОМ_2 ДОМ_3 |
.862443 .890267 .886055 .062145 .107230 .140876 |
.051643 .110351 .152603 .845786 .902913 .869995 |
| Общая дисперсия Доля общей дисп. |
2.356684 .392781 |
2.325629 .387605 |
Интерпретация факторной структуры. Теперь картина становится более ясной. Как и ожидалось, первый фактор отмечен высокими нагрузками на переменные, связанные с удовлетворенностью на работе, а второй фактор - с удовлетворенностью домом. Из этого вы должны заключить, что удовлетворенность, измеренная вашим вопросником, составлена из двух частей: удовлетворенность домом и работой, следовательно, вы произвели классификацию переменных.
Рассмотрим следующий пример, здесь к предыдущему примеру добавились четыре новых переменных Хобби.

На этом графике факторных нагрузок 10 переменных были сведены к трем факторам - фактор удовлетворенности работой (work), фактор удовлетворенности домом (home), и фактор удовлетворенности хобби (hobby/misc). Заметим, что факторные нагрузки для каждого фактора имеют сильно различающиеся значения для остальных двух факторов, но большие значения именно для этого фактора. Например, факторные нагрузки для переменных, относящихся к хобби (выделены зеленым цветом) имеют и большие, и малые значения для "дома" и "работы", но все четыре переменные имеют большие факторные нагрузки для фактора "хобби".
Косоугольные факторы. Некоторые авторы (например, Харман (Harman, 1976), Дженнрих и Сэмпсон (Jennrich, Sampson, 1966); Кларксон и Дженнрих (Clarkson, Jennrich, 1988)) обсуждали довольно подробно концепцию косоугольных (не ортогональных) факторов, для того чтобы достичь более простой интерпретации решений. В частности, были развиты вычислительные стратегии, как для вращения факторов, так и для лучшего представления "кластеров" переменных без отказа от ортогональности (т.е. независимости) факторов. Однако косоугольные факторы, получаемые с помощью этих процедур, трудно интерпретировать. Возвратимся к примеру, обсуждавшемуся выше, и предположим, что вы включили в вопросник четыре пункта, измеряющих другие типы удовлетворенности (Хобби). Предположим, что ответы людей на эти пункты были одинаково связаны как с удовлетворенностью домом (Фактор 1), так и работой (Фактор 2). Косоугольное вращение должно дать, очевидно, два коррелирующих фактора с меньшей, чем ранее, выразительностью, то есть с большими перекрестными нагрузками.
Иерархический факторный анализ. Вместо вычисления нагрузок косоугольных факторов, для которых часто трудно дать хорошую интерпретацию, вы можете использовать стратегию, впервые предложенную Томсоном (Thompson, 1951) и Шмидтом и Лейманом (Schmidt, Leiman, 1957), которая было подробно развита и популяризирована Верри (Wherry, 1959, 1975, 1984). В соответствии с этой стратегией, вначале определяются кластеры и происходит вращение осей в пределах кластеров, а затем вычисляются корреляции между найденными (косоугольными) факторами. Полученная корреляционная матрица для косоугольных факторов затем подвергается дальнейшему анализу для того, чтобы выделить множество ортогональных факторов, разделяющих изменчивость в переменных на ту, что относятся к распределенной или общей дисперсии (вторичные факторы), и на частные дисперсии, относящиеся к кластерам или схожим переменным (пунктам вопросника) в анализе (первичные факторы). Применительно к рассматриваемому примеру такой иерархический анализ может дать следующие факторные нагрузки:
| STATISTICA ФАКТОРНЫЙ АНАЛИЗ |
Вторичные и
первичные факторные нагрузки |
||
|---|---|---|---|
| Фактор | Вторич. 1 | Первич. 1 | Первич. 2 |
| РАБОТА_1 РАБОТА_2 РАБОТА_3 ДОМ_1 ДОМ_2 ДОМ_3 ХОББИ_1 ХОББИ_2 ХОББИ_3 ХОББИ_4 |
.483178 .570953 .565624 .535812 .615403 .586405 .780488 .734854 .776013 .714183 |
.649499 .687056 .656790 .117278 .079910 .065512 .466823 .464779 .439010 .455157 |
.187074 .140627 .115461 .630076 .668880 .626730 .280141 .238512 .303672 .228351 |
Внимательное изучение позволяет сделать следующие заключения:
Верри (Wherry, 1984) обсудил подробно примеры такого иерархического анализа и объяснил, каким образом могут быть получены значимые и интерпретируемые вторичные факторы.
Подтверждающий факторный анализ. Последние 15 лет так называемые методы подтверждения имели все большую популярность (например, см. Joreskog, Sorbom, 1979). Можно априори выбрать набор факторных нагрузок для некоторого числа ортогональных или косоугольных факторов, а затем проверить, может ли быть наблюдаемая корреляционная матрица воспроизведена при этом выборе. Подтверждающий факторный анализ может быть проведен с помощью Моделирования структурными уравнениями (SEPATH).
| В начало |
Другие результаты и статистики
Значения факторов. Вы можете оценить действительные значения факторов для отдельных наблюдений. Эти значения используются, когда желают провести дальнейший анализ факторов.
Воспроизведенные и остаточные корреляции. Дополнительным способом проверки числа выделенных факторов является вычисление корреляционной матрицы, которая близка исходной, если факторы выделены правильно. Эта матрица называется воспроизведенной корреляционной матрицей. Для того чтобы увидеть, как эта матрица отклоняется от исходной корреляционной матрицы (с которой начинался анализ), можно вычислить разность между ними. Полученная матрица называется матрицей остаточных корреляций. Остаточная матрица может указать на "несогласие", т.е. на то, что рассматриваемые коэффициенты корреляции не могут быть получены с достаточной точностью на основе имеющихся факторов.
Плохо обусловленные матрицы. Если имеются избыточные переменные, то нельзя вычислить обратную матрицу. Например, если переменная является суммой двух других переменных, отобранных для этого анализа, то корреляционная матрица для такого набора переменных не может быть обращена, и факторный анализ принципиально не может быть выполнен. На практике это происходит, когда вы пытаетесь применить факторный анализ к множеству сильно коррелированных (зависимых) переменных, что иногда случается, например, в исследованиях вопросников. Тогда вы можете искусственно понизить все корреляции в матрице путем добавления малой константы к диагональным элементам матрицы, и затем стандартизировать ее. Эта процедура обычно приводит к матрице, которая может быть обращена, и поэтому к ней применим факторный анализ; более того, эта процедура не влияет на набор факторов. Однако оценки оказываются менее точными.
| STATISTICA ФАКТОРНЫЙ АНАЛИЗ |
Вторичные и
первичные факторные нагрузки |
||
|---|---|---|---|
| Фактор | Вторич. 1 | Первич. 1 | Первич. 2 |
| РАБОТА_1 РАБОТА_2 РАБОТА_3 ДОМ_1 ДОМ_2 ДОМ_3 ХОББИ_1 ХОББИ_2 ХОББИ_3 ХОББИ_4 |
.483178 .570953 .565624 .535812 .615403 .586405 .780488 .734854 .776013 .714183 |
.649499 .687056 .656790 .117278 .079910 .065512 .466823 .464779 .439010 .455157 |
.187074 .140627 .115461 .630076 .668880 .626730 .280141 .238512 .303672 .228351 |
Внимательное изучение позволяет сделать следующие заключения:
Верри (Wherry, 1984) обсудил подробно примеры такого иерархического анализа и объяснил, каким образом могут быть получены значимые и интерпретируемые вторичные факторы.
| В начало |
![]()
(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA является торговой маркой StatSoft, Inc.