2М гистограммы. Этот термин был впервые использован Пирсоном в 1895 г.) 2М гистограммы являются графическими представлениями распределения частот выбранных переменных, на которых для каждого интервала (класса) рисуется столбец, высота которого пропорциональна частоте класса.

2М гистограммы - Висячие столбцы. Гистограмма висячих столбцов является "наглядным критерием проверки на нормальность распределения", который помогает определить области распределения, где возникают расхождения между наблюдаемыми и ожидаемыми нормальными частотами. В то время как стандартным способом представления подогнанного к наблюдаемому распределению нормального распределения является наложение на гистограмму наиболее подходящей нормальной кривой, гистограмма висячих столбцов предлагает противоположный способ: столбцы, представляющие наблюдаемые частоты для последовательных диапазонов значений, "подвешиваются" к наиболее подходящей нормальной кривой.

Если исследуемое распределение хорошо приближается нормальной кривой, то нижние ребра всех столбцов должны образовать прямую горизонтальную линию.

2М гистограммы - Простые. Эта гистограмма представляет собой столбчатую диаграмму распределения частот для выбранной переменной (если выбрано более одной переменной, то для каждой из них будет построен отдельный график).

2М гистограммы - С двойной осью Y. Гистограмму с двойной осью Y можно считать комбинацией двух по-разному масштабированных составных гистограмм. Для этой гистограммы можно выбрать две различные группы переменных. Для каждой из выбранных переменных будет изображено распределение частот, но частоты переменных из первого списка (называемого Левая ось Y) будут откладываться по левой оси Y, а частоты переменных из второго списка (называемого Правая ось Y) будут откладываться по правой оси Y. Имена всех переменных из двух списков будут внесены в условные обозначения и будут сопровождаться буквами Л или П, обозначающими соответственно левую или правую ось Y.

Этот график полезен для сравнения распределений переменных с разными частотами.

2М гистограммы - Составные. Составные гистограммы изображают распределение частот для нескольких переменных на одном 2М графике. В отличие от гистограмм с двойной осью Y частоты для всех переменных откладываются по левой оси Y.

Значения всех исследуемых переменных откладываются по одной оси X, что облегчает сравнение анализируемых переменных.

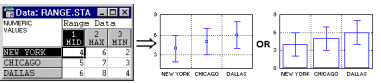
2М диаграммы диапазонов - Отрезки.
На диаграмме диапазонов такого типа диапазоны представлены "отрезками" с горизонтальными черточками на обоих концах (см. следующий рисунок). Средние точки обозначены маркерами точек.

2М диаграммы диапазонов - Прямоугольники.
На диаграмме  такого типа диапазон изображается в виде прямоугольника (верхняя сторона которого соответствует верхней границе диапазона, а нижняя сторона - нижней). Средние точки изображаются либо маркерами точек, либо горизонтальными линиями, "пересекающими" прямоугольник.

2М диаграммы диапазонов - Столбцы.
На диаграмме диапазонов такого типа средняя точка представлена столбцом (т.е. верх столбца задается значением средней точки), а диапазон (представленный "отрезком") накладывается на столбец.

2М диаграммы диапазонов - Столбцы ошибок. На   двумерной диаграмме диапазонов такого типа диапазоны или столбцы ошибок определяются исходными значениями выбранных переменных. Средние точки изображаются маркерами точек. Для каждого наблюдения строится один диапазон или столбец ошибок. В простейшем случае нужно выбрать три переменные, одна из которых будет соответствовать средним точкам, другая - верхним границам, а оставшаяся - нижним границам.

2М диаграммы размаха. На диаграммах размаха (этот термин был впервые использован Тьюки в 1970 г.) диапазоны или характеристики распределения значений выбранной переменной (или переменных) изображаются отдельно для групп наблюдений, заданных значениями категориальной (группирующей) переменной. Для каждой группы наблюдений вычисляется центральная тенденция (например, медиана или среднее) и вариационные статистики или статистики диапазона (например, квартили, стандартные ошибки или стандартные отклонения), и выбранные значения изображаются на диаграмме размаха выбранного типа. Также могут быть изображены точки выбросов.

2М диаграммы размаха/медианы (блоковые статистические графики). Этот тип блоковых статистических графиков представляет собой диаграмму размаха  для медиан (а также минимаксных значений и 25-й и 75-й процентилей) для столбцов или строк блока. Каждый прямоугольник отображает данные из одного столбца или строки.

2М диаграммы размаха - Отрезки. На диаграмме размаха такого типа диапазон (т.е. стандартная ошибка, стандартное отклонение, минимум-максимум или константа) представлен в виде отрезка (с горизонтальными черточками на обоих концах, как на показанном ниже рисунке).

2М диаграммы размаха - Прямоугольники. На диаграмме размаха такого типа вокруг средней точки (т.е. среднего или медианы) рисуется прямоугольник, который отражает выбранный диапазон (т.е. стандартную ошибку, стандартное отклонение, минимум-максимум или константу).

2М диаграммы размаха - Прямоугольники - Отрезки. На диаграммах размаха этого типа вокруг средней точки (т.е. среднего или медианы) рисуются прямоугольник, представляющий выбранный диапазон (т.е. стандартную ошибку, стандартное отклонение, минимум-максимум или константу), и отрезок, также отражающий выбранный диапазон, концы которого расположены вне прямоугольника (см. следующий рисунок).

2М диаграммы размаха/средние (блоковые статистические графики). Этот тип блоковых статистических графиков представляет собой диаграмму размаха  для средних (а также стандартных ошибок и стандартных отклонений) для столбцов или строк блока. Каждый прямоугольник отображает данные из одного столбца или строки.

2М диаграммы размаха - Столбцы ошибок. На статистических 2М диаграммах размаха такого типа диапазоны или столбцы ошибок вычисляются по данным. Центральная тенденция (например, медиана или среднее) и диапазон или вариационные статистики (например, значения минимума и максимума, квартили, стандартные ошибки или стандартные отклонения) вычисляются для каждой переменной, и выбранные значения представляются в виде столбцов ошибок.

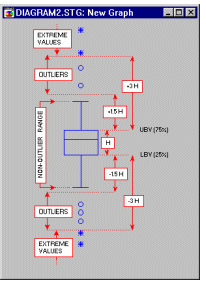
На показанном выше рисунке диапазоны  выбросов и крайних точек представлены на "классической" диаграмме размаха (о диаграммах размаха см. в работе Тьюки - Tukey, 1977).

2М диаграммы рассеяния. Диаграмма рассеяния визуализирует зависимость между двумя переменными X и Y (например, весом и высотой). Данные изображаются точками в двумерном пространстве, где оси соответствуют переменным (X  - горизонтальной, а Y - вертикальной оси).

Две координаты, которые определяют положение каждой точки, соответствуют значениям двух переменных.

См. также раздел  Сокращение объема выборки.

2М диаграммы рассеяния Вороного. Эта особая диаграмма рассеяния одной переменной является в большей степени аналитическим средством, нежели просто методом графического представления данных. Предлагаемые ею решения помогают моделировать множество явлений в естественных и социальных науках (см. Coombs, 1964 г.; Ripley, 1981 г.). Программа разделяет пространство между точками данных, представленными координатами X, Y в двумерном пространстве. Пространство между отдельными точками данных делится границами на такие области, каждая точка которых находится ближе к заключенной внутри точке данных, чем к любой другой соседней точке данных.

Использование этого метода сильно зависит от области исследования; однако во многих случаях к этой диаграмме полезно добавлять дополнительные измерения, используя категоризацию (см. следующий рисунок).

См. также раздел  Сокращение объема выборки.

2М диаграммы рассеяния - Простая. Простая диаграмма рассеяния визуализирует зависимость между двумя переменными X и Y (например, весом и высотой). Точки данных изображаются точками в двумерном пространстве, где оси соответствуют переменным. Две координаты (X и Y), которые определяют положение каждой точки, соответствуют значениям двух переменных для этой точки. Если две переменные сильно связаны, то множество точек данных принимает определенную форму (например, прямой линии или кривой). Если же переменные не связаны, то точки образуют "облако" (на следующем рисунке показан каьегоризованный график для двух типов данных).

Подгонка функций к диаграмме рассеяния позволяет выявить структуру связей между переменными (см. следующий рисунок).

Другие примеры диаграмм рассеяния можно найти в разделах Выбросы и Закрашивание. См. также раздел  Сокращение объема выборки.

2М диаграммы рассеяния - С двойной осью Y. Диаграмму рассеяния такого типа можно рассматривать как комбинацию двух составных диаграмм рассеяния для одной переменной X и двух различных наборов (списков) переменных Y. Для переменной X и каждой из переменных Y будет построена диаграмма рассеяния, но переменные из первого списка (называемого Левая ось Y) будут откладываться по левой оси Y, в то время как переменные из второго списка (называемого Правая ось Y), будут откладываться по правой оси Y. Имена всех переменных Y из двух списков будут включены в условные обозначения, сопровождаемые буквой (Л) или (П), обозначающей левую или правую ось Y соответственно.

Диаграммы рассеяния с двойной осью Y можно использовать для сравнения структуры нескольких корреляционных зависимостей путем изображения их на одном графике. При этом в силу независимости масштабов, используемых для двух списков переменных, этот график облегчает сравнение переменных, значения которых принадлежат разным диапазонам.

См. также раздел  Сокращение объема выборки.

2М диаграммы рассеяния - Составная. В отличие от простой диаграммы рассеяния, на которой одна переменная представлена по горизонтальной, а вторая - по вертикальной оси, составная диаграмма рассеяния состоит из нескольких зависимостей и изображает несколько корреляций : значения одной переменной (X) откладываются по горизонтальной оси, а по вертикальной оси откладываются значения нескольких переменных (Y). Для каждой переменной Y используется разный цвет и вид точек, который указан в условных обозначениях, так что на графике можно отличить зависимости для различных переменных.

Диаграмма рассеяния составного типа используется для сравнения структуры нескольких корреляционных зависимостей путем изображения их на одном графике, использующем один общий масштаб (например, для выявления основной структуры факторов или измерений при анализе дискриминантных функций).

См. также раздел  Сокращение объема выборки.

2М диаграммы рассеяния - Частоты . На диаграммах частот изображаются частоты перекрывающихся точек для двух переменных, чтобы наглядно представить веса точек данных или другие измеряемые параметры.

См. также раздел  Сокращение объема выборки.

2М круговая диаграмма. Термин "круговые диаграммы" впервые был использован Хаскеллом в 1922 году. На этих графиках пропорции отдельных значений переменной X представлены в виде круговых секторов.

2М линейные графики. На линейных графиках отдельные точки данных соединены линией.

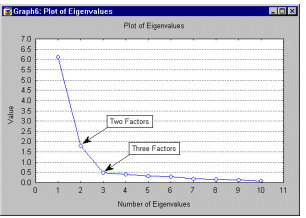
Эти графики являются простым способом представления и исследования последовательностей значений. Графики трассировочного типа можно использовать для воспроизведения следа (а не последовательности). Также линейные графики применяются для изображения непрерывных функций, теоретических распределений и т.п.

2М линейные графики - Агрегированные. Агрегированные линейные графики изображают последовательность средних для последовательных подмножеств выбранной переменной.

Можно выбрать число последовательных наблюдений, по которым будет вычислено среднее, а при необходимости диапазон значений в каждом подмножестве будет выделен значками типа отрезков. Агрегированные линейные графики используются для представления и исследования последовательностей большого числа значений.

2М линейные графики - Простые.  Простые линейные графики используются для представления и исследования последовательностей значений (обычно когда порядок значений является существенным).

Кроме того, линейные последовательные графики применяются при построении графиков непрерывных функций, таких как функции подгонки или теоретические распределения. Заметьте, что пустая ячейка данных (т.е. пропущенные данные) "разрывает" линию.

2М линейные графики - С двойной осью Y.  Линейный график с двойной осью Y можно рассматривать как комбинацию двух по-разному масштабированных составных линейных графиков. Для каждой выбранной переменной используется свой шаблон линии; и при этом все переменные, выбранные в списке Левая ось Y, будут откладываться по левой оси Y, а переменные, выбранные в списке Правая ось Y, будут откладываться по правой оси Y. Имена всех переменных будут указаны в условных обозначениях вместе с буквой Л для переменных, относящихся к левой оси Y, и с буквой П для переменных, относящихся к правой оси Y.

Линейный график с двойной осью Y можно использовать для сравнения последовательностей значений нескольких переменных, накладывая их линейные представления на один график. В то же время в силу независимости шкал, используемых для двух осей, этот график может облегчить сопоставление переменных трудно поддающихся сравнению (т.е. имеющих значения в разных диапазонах).

2М линейные графики - Составные.   В отличие от простых линейных графиков, на которых представлена последовательность значений одной переменной, на составном линейном графике изображаются несколько последовательностей значений (переменных). Для каждой переменной используется и указывается в условных обозначениях свой шаблон и цвет линии.

Этот тип линейных графиков используется для сравнения последовательностей значений нескольких переменных (или нескольких функций) путем изображения их на одном графике, использующем один общий масштаб (например, для сравнения нескольких одновременных экспериментальных процессов, социальных явлений, цен акций или товаров, форм кривых текущих характеристик и т.п.).

2М линейные графики - Трассировочные XY.  На трассировочных графиках сначала строится диаграмма рассеяния двух переменных, а затем отдельные точки данных соединяются линией (в порядке их считывания из файла данных). В этом смысле трассировочные графики визуализируют "путь" последовательного процесса (движение, изменение явления во времени и т.п.).

2М линейные графики (профили наблюдений).  В отличие от простых линейных графиков, на которых значения одной переменной изображаются в виде одной линии (точки данных соединяются линией), на линейных графиках профилей наблюдений одна линия рисуется для значений выбранных переменных для одного наблюдения (строки), т.е. для каждого из выбранных наблюдений строится один линейный график. Линейные графики профилей наблюдений являются простым способом наглядного представления значений одного наблюдения (например, результатов нескольких тестов).

2М линейный график (или категоризованный линейный график) медиан с квантилями и минимаксными диапазонами
С помощью диалогового окна Статистические 2М диаграммы размаха можно построить 2М линейный график медиан с квантилями и минимаксными столбцами диапазонов. В этом окне нужно выбрать медиану в качестве средней точки, процентили (с коэффициентом 25) для прямоугольника, и мин-макс для отрезка. Наконец, остается пометить поле Соединить средние точки, чтобы медианы на графике были соединены линией.
Таким же образом можно построить категоризованный 2М линейный график медиан с квантилями и минимаксными диапазонами, выбирая те же пункты в диалоговом окне Статистические категоризованные диаграммы размаха.

2М последовательные/наложенные графики - Зонные.   На  графике этого типа последовательности значений каждой выбранной переменной будут представлены последовательными областями, расположенными одна над другой.

2М последовательные/наложенные графики - Линейные. На  графике этого типа последовательности значений каждой выбранной переменной будут представлены последовательными линиями, расположенными одна над другой.

2М последовательные/наложенные графики - Смешанные ступенчатые.  На  графике этого типа последовательности значений переменных, выбранных в первом списке,  будут представлены последовательными ступенчатыми областями, расположенными одна на другой, а последовательности значений переменных, выбранных во втором списке,  - последовательными ступенчатыми линиями, расположенными одна над другой (над областью, отвечающей последней переменной из первого списка).

2М последовательные/наложенные графики - Смешанные линейные. На  графике этого типа последовательности значений переменных, выбранных в первом списке, будут представлены последовательными областями, расположенными одна на другой, а последовательности значений переменных, выбранных во втором списке, - последовательными линиями, расположенными одна над другой (над областью, отвечающей последней переменной из первого списка).

2М последовательные/наложенные графики - Столбчатые диаграммы.  На  графике этого типа последовательности значений каждой выбранной переменной будут представлены последовательными сегментами вертикальных столбцов, расположенных друг над другом.

2М последовательные/наложенные графики - Ступенчатые.  На  графике этого типа последовательности значений каждой выбранной переменной будут представлены ступенчатыми линиями, расположенными одна над другой.

2М последовательные/наложенные графики - Ступенчатые зонные.  На графике этого типа последовательности значений каждой выбранной переменной будут представлены ступенчатыми областями, расположенными одна над другой.

2М столбчатые диаграммы.   На столбчатой диаграмме последовательность значений представлена в виде столбцов (одному наблюдению соответствует один столбец). Если выбрано несколько переменных, то для каждой из них будет построен отдельный график. Можно построить составную диаграмму, где все переменные будут отображены одновременно в виде групп столбцов (одна группа для каждого наблюдения, как на следующем рисунке).