Левенберга-Маркара алгоритм. Метод нелинейной оптимизации, использующий для поиска минимума комбинированную стратегию - линейную аппроксимацию и градиентный спуск; переключение с одного метода на другой происходит в зависимости от того, была ли успешной линейная аппроксимация; такой подход называется моделью доверительных областей (Levenberg, 1944; Marquardt, 1963; Bishop, 1995; Shepherd, 1997; Press et. al., 1992).

См. также раздел  Нейронные сети.


Линейная подгонка (2М графики). К точкам 2М диаграммы рассеяния подгоняется линейная функция (например, Y = a + bX).


Линейная функция активации. Тождественная функция активации: выходной сигнал элемента совпадает с его уровнем активации.

См. также раздел  Нейронные сети.


Линейное моделирование. Аппроксимация дискриминантной или регрессионной функции с помощью гиперплоскости. Для этой гиперплоскости с помощью "простых" вычислений может быть найдено глобально оптимальное положение, однако таким образом нельзя построить адекватные модели для многих реальных задач.

См. также раздел  Нейронные сети.

Линейное сглаживание (3М графики). К точкам 3М диаграммы рассеяния подгоняется линейная функция (например, Z = a + bX + cY).


Линейные элементы. Элементы, имеющие линейную пост-синаптическую (PSP) функцию. Уровень активации такого элемента представляет собой взвешенную сумму его входов, из которой вычитается пороговое значение - это называется также скалярным произведением или линейной комбинацией. Этот тип элементов обычно используется в многослойных персептронах. Несмотря на название, линейные элементы могут иметь нелинейные функции активации.

См. также раздел  Нейронные сети.


Линия n-точечного скользящего среднего. Каждая точка на линии скользящего среднего представляет среднее соответствующей выборки и n-1 числа предыдущих выборок. Таким образом, линия сглаживает модель средних по выборкам, позволяя специалисту по контролю качества выделить тренды. Вы можете определить число выборок (n), которые надо усреднить.

Дополнительно см. раздел Временные ряды.


Линия экспоненциально взвешенного скользящего среднего. Этот способ сглаживания можно рассматривать как обобщение простого скользящего среднего. Каждая точка на графике вычисляется как:
zt = *x-bart + (1-)*z t-1
В этой формуле каждое значение zt вычисляется как (лямбда) умноженная на соответствующее среднее x- bart, плюс 1 минус , умноженная на предыдущее значение на графике. Параметр (лямбда) должен быть больше 0 и меньше 1. Вы можете узнать в этой формуле обычное экспоненциальное сглаживание. Не вдаваясь в детали (см. Montgomery, 1985, стр. 239), заметим, что в этом методе выбираются экспоненциально убывающие веса для наблюдений (отстоящих от текущего). Этот тип линии скользящего среднего также сглаживает случайные различия в средних разных выборок и позволяет инженеру более отчетливо обнаружить тренд.


Логарифмическая подгонка. При выборе этого варианта  к данным подгоняется логарифмическая функция следующего вида:

y = q*[logn(x)] + b


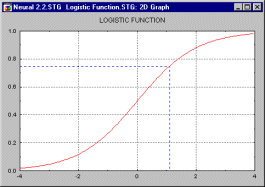
Логистическая функция. Функция с S-образной (сигмоидной) формой графика, принимающая значения в интервале (0,1). См. также Логистическое распределение.

Логистическая функция

Логистическое распределение. Логистическое распределение имеет следующую функцию плотности:

f(x) = (1/b)*e-(x-a)/b * [1+e-(x-a)/b]-2

где
a    - среднее распределения
b    - параметр масштаба
e     - число Эйлера (2.71...)

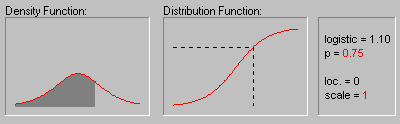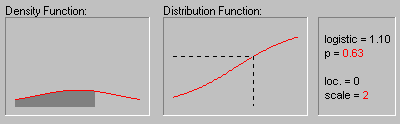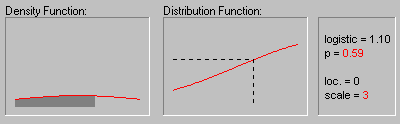
Логистическое распределение

На предыдущем графике показано изменение формы логистического распределения при значении параметра  положения, равном 0, для различных значений  параметра масштаба 1, 2 и 3.


Логлинейный анализ. Логлинейный анализ предоставляет "высоконаучный" подход к рассмотрению таблиц сопряженности (при проведении разведочного анализа данных и проверке гипотез), и иногда рассматривается в качестве эквивалента дисперсионного анализа для таблиц частот. Более точно, он позволяет пользователю проверить статистическую значимость влияния различных факторов (например, пол, место жительства и т.п.) и их взаимодействий при построении таблиц сопряженности (обсуждение методов проверки статистической значимости см. в разделе Элементарные понятия статистики).

Для получения дополнительной информации см. раздел  Логлинейный анализ.


Логнормальное распределение. Логнормальное распределение (этот термин был впервые использован Гаддумом в 1945 г.) имеет следующую функцию плотности:

f(x) = 1/[x(2)1/2] * exp(-[log(x)-µ]2/22)
0 x <
µ > 0
> 0

где
µ     - параметр масштаба
    - параметр (формы)
e    - число Эйлера (2.71...)

На рисунке показано логнормальное распределение для µ равного 0 и разных значений сигма: .10, .30, .50, .70 и .90.


Ложные корреляции. Это корреляции, которые вызваны влиянием одной или нескольких "других" переменных. Например, можно обнаружить сильную положительную связь (корреляцию) между разрушениями, вызванными пожаром, и числом пожарных, тушивших пожар. Следует ли заключить, что пожарные вызывают разрушения? Конечно, наиболее вероятное объяснение этой корреляции состоит в том, что размер пожара (внешняя переменная, которую забыли включить в исследование) оказывает влияние, как на масштаб разрушений, так и на числе привлеченных пожарных (т.е. чем больше пожар, тем большее количество пожарных вызывается на его тушение). Хотя этот пример довольно прозрачен, в реальности при исследовании корреляций альтернативные причинные объяснения часто даже не рассматриваются. При этом главная проблема заключается в том, что мы обычно не знаем даже того, что "скрытый" агент существует. Однако в случаях, когда мы не знаем, какие именно переменные рассматривать, мы можем использовать частные корреляции, чтобы управлять влиянием выбранных переменных (т.е. задавать их конкретные значения).

См. также разделы  Корреляции, Частные корреляции, Основные статистики, Множественная регрессия, Моделирование структурными уравнениями (SEPATH).


Локальные минимумы. В большинстве практических приложений локальные минимумы функции потерь приводят к неправдоподобно большим или неправдоподобно малым значениям параметров с очень большими стандартными ошибками. Симплекс-метод нечувствителен к таким минимумам; поэтому он может быть использован для отыскания подходящих начальных значений для сложных функций.


Лямбда. Лямбда определяется как геометрическая сумма 1 минус квадрат канонической корреляции и называется также лямбда Уилка. Квадрат канонической корреляции является оценкой доли дисперсии, общей между двумя каноническими переменными, поэтому 1 минус это значение равно оценке необъясненной доли дисперсии. Лямбда используется в качестве статистики критерия значимости квадрата канонической корреляции и имеет распределение хи-квадрат:

2 = [-N -1 - {.5(p+q+1)}] * loge

где
N    число наблюдений
p   число переменных справа (в правом списке)
q   число переменных слева (в левом списке)