0
Гамма-распределение. Гамма- распределение (этот термин был впервые использован в работе Везерберна - Weatherburn, 1946) определяется следующим образом:
f(x) = (x/b)c-1 * e(-x/b) * [1/b ![]() (c)]
(c)]
0 ![]() x, b > 0, c > 0
x, b > 0, c > 0
где
![]() - гамма-функция
- гамма-функция
b - параметр масштаба
c - параметр (формы)
e - число Эйлера (2.71...)

На рисунке показано гамма-распределение
при изменении значений параметра формы от 1 до 6.
Гармоническое среднее. Гармоническое среднее - это итоговая статистика, используемая в анализе частот, которая вычисляется как:
H = n * 1/![]() (1/xi)
(1/xi)
где
n - число наблюдений
(объем выборки).
Гауссовское
распределение. То же, что и нормальное распределение.
Имеет форму колокола.
Генетический алгоритм. Алгоритм поиска оптимальной битовой строки, который случайным образом выбирает начальную популяцию таких строк и затем подвергает их процессу искусственных мутаций, скрещивания и отбора по аналогии с естественным отбором (Goldberg, 1989).
См. также раздел Нейронные
сети.
Генетический
алгоритм отбора входных данных. Применение
генетического алгоритма к
нахождению "оптимального" набора входных
переменных путем построения битовых масок,
обозначающих, какие из переменных следует
оставить на входе, а какие удалить (Goldberg, 1989). Этот
метод реализован в пакете Нейронные сети STATISTICA
и может служить этапом построения модели, на
котором отбираются наиболее "существенные"
переменные; затем отобранные переменные
используются для построения обычной
аналитической модели (например, линейной
регрессии или нелинейного оценивания).
Геометрическое распределение. Геометрическое распределение (этот термин был впервые использован в работе Феллера - Feller, 1950 г.) определяется следующим образом:
f(x) = p*(1-p)x
где
p - вероятность
наступления определенного события (например,
успеха)
Геометрическое среднее. Геометрическое среднее - это итоговая статистика, полезная при нелинейной шкале измерений, которая вычисляется как:
G = (x1*x2*...*xn)1/n
где
n - число наблюдений
(объем выборки).
Гиперболический
тангенс (tanh). Симметричная функция с
S-образной (сигмоидной) формой графика;
используется как альтернатива логистической
функции.
Гиперплоскость.
N-мерный аналог прямой линии или плоскости,
делит N+1-мерное пространство на две части.
См. Нейронные сети.
Гиперсфера. N-мерный
аналог окружности или сферы. См. Нейронные сети.
Главных компонент анализ. Линейный метод понижения размерности, в котором определяются попарно ортогональные направления максимальной вариации исходных данных, после чего данные проектируются на пространство меньшей размерности, порожденное компонентами с наибольшей вариацией (Bishop, 1995).
См. Факторный анализ и Нейронные сети.
Горизонт (для нейронных сетей). У нейронных сетей для анализа временных рядов - число шагов по времени, считая от последнего входного значения, на которое нужно спрогнозировать значения выходной переменной.
См. также главу по нейронным
сетям.
Градиентный
спуск. Совокупность методов оптимизации
нелинейных функционалов (например, функции
ошибок нейронной сети,
когда веса сети рассматриваются как аргументы
функции), где с целью поиска минимума происходит
последовательное продвижение во все более
низкие точки в пространстве поиска.
График каменистой осыпи, критерий каменистой осыпи. Собственные значения для последовательных факторов можно отобразить на обычном линейном графике. Для графического определения оптимального числа факторов Каттел (Cattell, 1966) предложил использовать график каменистой осыпи.
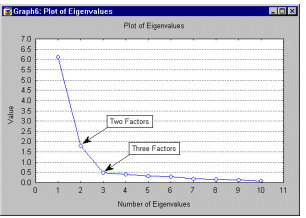
Критерий каменистой осыпи состоит в поиске точки, где убывание собственных значений замедляется наиболее сильно. Справа от этой точки находится, по-видимому, только "факторная осыпь"; "осыпь" - это геологический термин для обломков, которые скапливаются в нижней части каменистого склона. Таким образом, число выделенных факторов не должно превышать количество факторов слева от этой точки.
За дополнительной информацией о процедурах
определения оптимального числа факторов
обратитесь к обзору
результатов анализа главных компонент в
главе о факторном анализе и к разделу Задание размерности в
главе о многомерном шкалировании.
График
поверхности (по исходным данным). На этом
последовательном графике изображается
подогнанная к каждой точке данных сглаженная
сплайнами поверхность. Последовательные
значения каждой серии откладываются по оси X,
а сами последовательные серии представлены
вдоль оси Y.
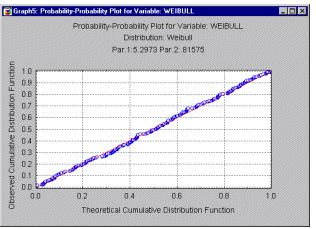
Графики вероятность-вероятность. Подгонку теоретического распределения к наблюдаемым данным можно зрительно оценить на графике вероятность-вероятность (также называемом вероятностным графиком, см. следующий рисунок). Графики вероятность-вероятность (или В-В) показывают связь функций наблюдаемого и теоретического кумулятивных распределений. Как и для графика квантиль-квантиль, значения переменной сначала упорядочиваются по возрастанию. Наблюдению с номером i соответствует значение i/n на одной оси (т.е. функция наблюдаемого кумулятивного распределения) и значение F(x(i)) на другой оси, где F(x(i)) есть значение функции теоретического кумулятивного распределения для соответствующего наблюдения x(i). Если теоретическое распределение хорошо приближает наблюдаемое распределение, то все точки графика должны попасть на диагональную линию.
Графики квантиль-квантиль. Подгонку теоретического распределения к наблюдаемым данным можно зрительно оценить на графике квантиль-квантиль (или К-К) (также называемом графиком квантилей).
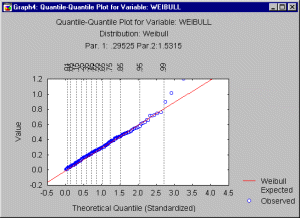
На этом графике показана связь между наблюдаемыми значениями переменных и теоретическими квантилями. Если наблюдаемые значения попадают на прямую линию, то теоретическое распределение хорошо подходит к наблюдаемым данным. Для построения графика К-К программа сначала упорядочивает по возрастанию n точек наблюдаемых данных:
x1 ![]() x2
x2 ![]() ...
... ![]() xn
xn
Эти наблюдаемые значения откладываются по одной из осей графика; по другой оси откладываются следующие значения:
F-1((i-radj) / (n+nadj))
где i есть ранг
соответствующего наблюдения, radj
и nadj - корректировки (![]() 0.5), а F-1
есть обратный вероятностный интеграл для
соответствующего стандартизованного
распределения. Получившийся график (см. выше)
представляет собой диаграмму рассеяния
наблюдаемых и ожидаемых (стандартизованных)
значений при соответствующем заданном
распределении. Отметим также, что корректировки radj и nadj
обеспечивают попадание p-значения для
обратного вероятностного интеграла в интервал
от 0 до 1, не включающий 0 и 1 (см. Chambers, Cleveland, Kleiner,
Tukey, 1983).
0.5), а F-1
есть обратный вероятностный интеграл для
соответствующего стандартизованного
распределения. Получившийся график (см. выше)
представляет собой диаграмму рассеяния
наблюдаемых и ожидаемых (стандартизованных)
значений при соответствующем заданном
распределении. Отметим также, что корректировки radj и nadj
обеспечивают попадание p-значения для
обратного вероятностного интеграла в интервал
от 0 до 1, не включающий 0 и 1 (см. Chambers, Cleveland, Kleiner,
Tukey, 1983).
Группирующая
(или кодирующая) переменная. Группирующая
(или кодирующая) переменная используется для
разбиения на группы наблюдений в файле данных.
Обычно группирующая переменная является
категориальной, т.е. содержит дискретные
значения, например, 1, 2, 3, ...,
| Группа | Результат 1 | Результат 2 |
|---|---|---|
| 1 3 2 2 |
383.5 726.4 843.7 729.9 |
4568.4 6752.3 5384.7 6216.9 |
или несколько текстовых значений, например, MALE,
FEMALE.
| Группа | Результат 1 | Результат 2 |
|---|---|---|
| MALE FEMALE FEMALE MALE |
383.5 726.4 843.7 729.9 |
4568.4 6752.3 5384.7 6216.9 |
Значения такой переменной называются кодами (они могут быть
целочисленными или целочисленными с текстовыми
эквивалентами).
Групповое
программное обеспечение. Это программное
обеспечение, которое дает возможность группе
пользователей, использующих компьютерную сеть,
одновременно работать над конкретным проектом.
Оно содержит средства для организации связи
(электронную почту), для совместной обработки
документов, проведения анализа, создания отчетов
и статистической обработки данных, а также
календарного планирования и наблюдения. При этом
обрабатываемые документы могут содержать
информацию любого типа: текст, картинки или
мультимедийный формат. См. также Программное
обеспечение на производстве.
Групповые
контрольные карты. При построении
групповой контрольной
карты на одну и ту же карту наносятся данные
для нескольких потоков наблюдаемых значений
непрерывной переменной или альтернативного
признака - характеристики качества. Для каждой
выборки, содержащей изменения контролируемой
характеристики, на карту наносятся две точки, в
результате чего на ней образуются две линии.
Верхняя из этих линий представляет собой график
наиболее высоких средних значений в каждой
выборке для всех нанесенных на карту потоков
переменных или альтернативных признаков, а
нижняя - подобный график наименьших средних
значений каждой выборки. Для каждой выборки
верхняя и нижняя точка соответствуют
максимальному и минимальному средним значениям
нескольких переменных или альтернативных
признаков, нанесенных на карту. Если данные
экстремальные значения не выходят за рамки
заданных контрольных
пределов, то очевидно, что все остальные
выборочные средние также находятся внутри
диапазона, ограниченного контрольными
пределами. Следовательно, многопоточные групповые
карты позволяют быстро определить, не началась
ли разладка процесса в одном или нескольких
потоках процесса или контролируемых
характеристик, не переходя к проверке всех
измерений подряд.