Два значения (для нейронных сетей). Способ кодирования значений номинальных переменных, принимающих только два значения, при котором номинальной переменной соответствует один входной или выходной элемент, который может быть активен или неактивен.

См. раздел Нейронные сети.

Двумерное нормальное распределение. Две переменные имеют двумерное нормальное распределение, если для каждого фиксированного значения одной переменной соответствующие значения другой переменной нормально распределены. Функция двумерного нормального распределения для пары переменных (X и Y) определяется следующим образом:

f(x,y) = {1/[212 * (1-)1/2]} * exp[-1/2(1-2)] * {[(x-1)/1]2 -

2[(x-1)/1] * [(y-2)/2] + [(y-2)/2]2}

- < x < , - < y < , - < 1 < , - < 2 < , 1 > 0, 2 > 0 и -1 < < 1

где
₁, ₂  - соответствующие средние случайных величин X и Y
₁, ₂  - соответствующие стандартные отклонения случайных величин X и Y
  - коэффициент корреляции X и Y
e         - число Эйлера e (2.71...)
   - число пи (3.14...)

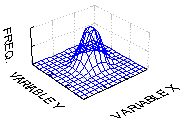
См. также разделы Нормальное распределение, Элементарные понятия статистики (нормальное распределение).

Декартовы координаты. Декартовы (или прямоугольные) координаты (x, y или x, y, z) представляют собой направленные расстояния от двух (или трех) перпендикулярных осей.

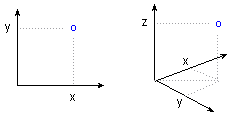
Положение точки в пространстве определяется соответствующими координатами на осях X и Y (или X, Y и Z).

См. также Полярные координаты.

Дельта - дельта с чертой. Эвристическая модификация алгоритма обратного распространения для нейронных сетей, имеющая цель автоматически корректировать скорость обучения по каждой из координатных осей в пространстве поиска с тем, чтобы учесть особенности его топологии (Jacobs, 1988; Patterson, 1996).

Деревья классификации. Методы деревьев классификации предназначены для прогнозирования принадлежность наблюдений (объектов) к тому или иному классу значений зависимой категориальной переменной на основании значений одной или нескольких предикторных переменных.

Подробное описание этих методов дается в главе   Деревья классификации.

Диаграмма Вороного (мозаика). На мозаичной диаграмме Вороного значения двух переменных X и Y изображаются, как на диаграмме рассеяния, а затем пространство между отдельными точками данных делится границами, окружающими каждую точку данных, на области по следующему принципу: каждая точка области находится ближе к заключенной внутри точке данных, чем к любой другой соседней точке данных.

Диаграмма кластеров (для нейронных сетей). Точечная диаграмма, на которой наблюдения из разных классов представлены на плоскости. Координаты на плоскости соответствуют выходным уровням некоторых элементов сети. См. также раздел Кластерный анализ.

Диаграмма отклонений. На этом графике данные интерпретируются как координаты X, Y, Z и отображаются в трехмерном пространстве в виде "отклонений" от заданного уровня на оси Z.

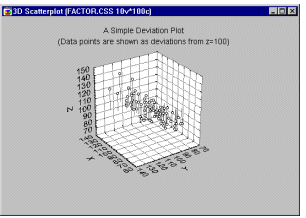
Диаграмма отклонений похожа на  пространственный график. Однако в отличие от него на этой диаграмме не показана в явном виде сама "плоскость отклонений" (здесь оси X-Y всегда находятся в нижнем положении).  Этот тип графического представления данных позволяет исследовать структуру трехмерных зависимостей с помощью "рассечения" данных на произвольном горизонтальном уровне.

См. также раздел  Вращение данных (в трехмерном пространстве)  в главе   Графические методы анализа.

Диапазон без выбросов. Диапазон без выбросов - это диапазон значений на 2М диаграммах размаха, 3М последовательных графиках - диаграммах размаха или категоризованных диаграммах размаха, которые попадают ниже верхней границы для выбросов (например, +1.5 * высоту прямоугольника) и выше нижней границы для выбросов (например, -1.5 * высоту прямоугольника).


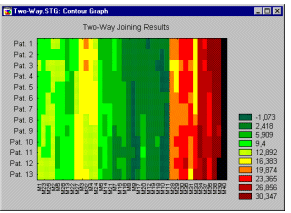
Дискретная карта линий уровня для исходных данных. Этот последовательный график можно считать 2М проекцией 3М ленточной диаграммы. Каждая точка данных здесь представлена прямоугольной областью; значениям (или диапазонам значений точек данных) соответствуют различные цвета и/или шаблоны областей (диапазоны указаны в условных обозначениях). Значения внутри каждой серии откладываются по оси X, а сами серии - по оси Y.

Дискриминантный анализ. Дискриминантный анализ используется для принятия решения о том, какие переменные дискриминируют или разделяют объекты на две или более естественно возникающих  групп (его используют как метод проверки гипотез или как метод разведочного анализа).   Предположим, исследователь в области образования хочет определить, какие переменные относят выпускника средней школы к одной из трех категорий: (1) поступающие в колледж, (2) поступающие в профшколу или (3) отказывающиеся от дальнейшего образования или профессиональной подготовки. Для этой цели исследователь мог собирать данные о различных переменных до окончания учащимися школы. После выпуска большинство учащихся естественно должно попасть в одну из перечисленных выше категорий. Затем можно использовать дискриминантный анализ для определения, какие переменные дают наилучшее предсказание о выборе учащимися их дальнейшего пути и в дальнейшем использовать эти результаты, например, для прогноза судьбы учеников следующего года выпуска.

Подробнее см. главы Дискриминантный анализ и Деревья классификации.

Дисперсионный анализ. Целью дисперсионного анализа (ANOVA) является проверка значимости различия между средними с помощью сравнения (т.е. анализа) дисперсий. А именно, разделение общей дисперсии на несколько источников (связанных с различными эффектами в плане), позволяет сравнить дисперсию, вызванную различием между группами, с дисперсией, с дисперсией, вызванной внутригрупповой изменчивостью. При истинности нулевой гипотезы (о равенстве средних в нескольких группах наблюдений, выбранных из генеральной совокупности), оценка дисперсии, связанной с внутригрупповой изменчивостью, должна быть близкой к оценке межгрупповой дисперсии.

Подробнее см. главу   Дисперсионный анализ.

Дисперсия. Дисперсия  популяции (термин впервые введен Фишером, 1918) вычисляется по формуле:

² = (x_i-µ)²/N

где
µ     - среднее
N    - размер популяции.
Несмещенная оценка дисперсии вычисляется по формуле:

s² = (x_i-xbar)²/n-1

где
xbar   - выборочное среднее
n        - число наблюдений в выборке.

См. также  Описательные статистики.

Добавление наблюдений и/или переменных. Действие, в результате которого в конец набора данных ("дно" или правый край) добавляются соответственно новые наблюдения (строки) и/или переменные (столбцы). Стоки или столбцы можно также вставлять в любое место в наборе данных.

Добыча данных. StatSoft определяет область добычи данных (Data Mining) как совокупность методов аналитической обработки больших массивов данных (часто связанных с деловой активностью или рыночными показателями) с целью выявить в них значимые закономерности и/или систематические связи между переменными, которые затем можно применить к новым совокупностям данных.

В методах добычи данных используются многие принципы и приемы, которые принято относить к разведочному анализу данных(РАД).
Дополнительную информацию см. в главе Добыча данных.


Доверительные пределы. То же самое, что и  доверительные интервалы. Применительно к нейронным сетям задают пороги принятия и отвержения, которые используются в задачах классификации при решении вопроса о том, относится ли данный выходной набор к конкретному классу. Используются в соответствии с типом функции преобразования выходной переменной (Один-из-N, Два значения, Кохонена и т.д.).

Доверительный интервал. Доверительные интервалы для некоторой статистики (например, среднего значения или линии регрессии) показывают диапазон вокруг значения статистики, в котором находится истинное значение этой статистики (с определенным уровнем надежности или доверия см. также раздел Элементарные понятия статистики).

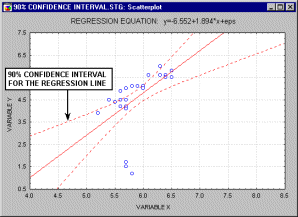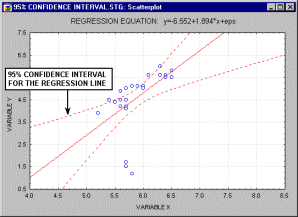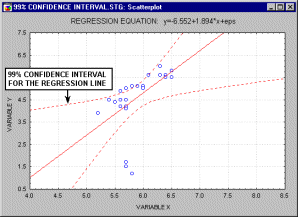
Например, на показанном выше рисунке последовательно отображаются 90%, 95% и 99% доверительные интервалы для линии регрессии.

Доверительный интервал для среднего. Доверительные интервалы для среднего задают область вокруг среднего, в которой с заданным уровнем доверия содержится "истинное" среднее популяции (см. также Элементарные понятия статистики). В некоторых статистических или математических программных пакетах (например, в системе STATISTICA) вы можете построить доверительные интервалы для любого p-уровня; например, если среднее в вашей выборке равно 23, а нижняя и верхняя границы для p=.05 равны 19 и 27 соответственно, то вы можете заключить, что с  95% вероятностью среднее выборки больше 19 и меньше 27. Если вы установите меньшее значение p-уровня, то интервал будет шире, и увеличится "уверенность" в оценке, и наоборот; как мы знаем из прогнозов погоды, чем "неопределеннее" прогноз (т.е. шире доверительный интервал), тем скорее он сбудется. Заметим, что ширина доверительного интервала зависит от размера выборки и дисперсии наблюдений. Вычисление доверительных интервалов основывается на предположении, что переменная в совокупности нормально распределена. Эта оценка может быть неверной, если это предположение не выполнено, и пока размер выборки мал, например, n меньше 100.