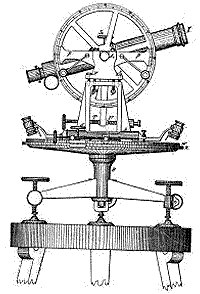
Une grande réalisation du XVIII ème siècle fut la "grande mesure trigonométrique" de l'Inde britannique. Les deux plus grands théodolites jamais construits furent réalisés pour ce projet, véritables monstres avec des plateaux circulaires de 36 pouces de large, sur lesquels les graduations étés lues avec une précision exceptionnelle par 5 microscopes. Chacun dans son coffre pesait une demie tonne et il fallait 12 hommes pour la transporter . Grâce à eux, ce projet a découpé le pays en multiples côtés de triangles du nord au sud et d'est en ouest (les secteurs entre les côtés ont été laissés pour après) et cela a pris des décennies pour être mené à bien.
En 1843 Andrew Scott Waugh a pris la charge ce projet en tant qu' Arpenteur - Général, et étudiât en particulier les crêtes de l'Himalaya au nord de l'Inde. En raison des nuages et de la brume ces crêtes sont rarement vues des terres situées en contrebas, et peu de mesures avaient été réalisées sous contrôle de la vue jusqu'en 1847. Et même après, les résultats ont dû être laborieusement analysés par des "ordinateurs" dans les bureaux de vérification : non pas par des machines, mais par les personnes qui avaient exécuté tous les calculs trigonométriques.
L'histoire dit qu'en 1852, le calculateur en chef, Radanath Sikhdar, rendit visite au directeur du projet et lui annonçât : "Monsieur, nous avons découvert la plus haute montagne du monde." A une distance de plus de 100 milles (160 kilomètres), la crête a été observée depuis six stations différentes, et " l'observateur n'a jamais suspecté qu'il visionnait dans son télescope le point le plus élevé de la terre." à l'origine elle est désignée comme "crête XV" dans le rapport, mais en 1856 Waugh lui donna le nom de Sir George Everest, son prédécesseur comme chef arpenteur. Everest fut celui qui commanda et utilisa pour la première fois ces théodolites géants ; ils sont maintenant exposés au musée du relevé de l'Inde à Dehra Dum.
De nos jours la localisation d'un point sur la terre peut être déterminée avec exactitude en utilisant le "système de positionnement global"
(GPS) qui recourt à 24 satellites aux orbites précises, émettant constamment leurs positions. Un petit instrument électronique tenu en main reçoit leurs signaux et donne la position à moins de 10-20 mètres (encore plus exactement pour les militaires, commanditaires du système).Cela implique beaucoup de trigonométrie, mais c'est l'ordinateur de l'instrument qui s'en occupe : tout ce que vous avez à faire est d'enfoncer les boutons appropriés.
Maintenant que vous connaissez un peu les utilisations de la trigonométrie, vous êtes parés pour en étudier l'essentiel