Эвристика. В противоположность алгоритму (который описывает вполне определенный набор операций для получения конкретного результата), эвристики - это общие рекомендации или советы, основанные на статистической очевидности (например, "курение сокращает вашу жизнь", "мужчины с высшим образованием с большей вероятностью положительно отнесутся к этой рекламе, чем...") или теоретических рассуждениях (например, "механизм синтеза витамина X, в нашем понимании, позволяет утверждать, что употребление в пищу продукта Y уменьшает дефицит X"). Подробнее о понятии эвристики см. работу Kahneman, Slovic, & Tversky, 1982.

См. также Добыча данных, Нейронные сети, алгоритм.

Экспоненциальная функция. При выборе этого метода подгонки к данные аппроксимируются экспоненциальной функцией следующего вида:

y = b*exp(q*x)

Экспоненциальное распределение. Экспоненциальное распределение определяется следующим образом:

f(x) = * e^-x
0 x < , > 0

где
(лямбда) - параметр экспоненциальной функции (альтернативной параметризацией является параметр масштаба b=1/)
 e      - основание натуральных логарифмов (2.71...)

На этом графике показано экспоненциальное распределение с  лямбда равным 1.

Экспоненциальные распределения (семейство). Семейство функций распределения, включающих экспоненциальные члены. В качестве частных случаев содержит наиболее важные типы распределений, встречающиеся в реальных задачах (в том числе нормальное или гауссово распределение, альфа- и бета-распределения). См. также Нейронные сети.

Экстраполяция. Прогнозирование неизвестных значений путем продолжения функций за границы области известных значений.

Экстремальное распределение (тип I, Гумбеля). Экстремальное распределение, называемое распределением I-го типа (этот термин был впервые использован Либлайном в 1953 г.), имеет следующую функцию плотности:

f(x) = 1/b * e^-(x-a)/b * e^{-e-(x-a) / b}
- < x <
b > 0

где
a    - параметр положения
b    - параметр масштаба
e    - основание натуральных логарифмов (2.71...)
Это распределение иногда называют распределением наибольшего экстремального значения.

См. также Анализ процессов.

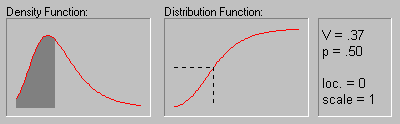
На рисунке показана форма распределения экстремальных значений для параметра положения, равного 0, и параметра масштаба, равного 1.

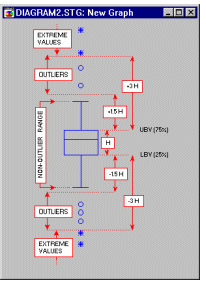
Экстремальные значения (на диаграммах размаха). Значения, находящиеся далеко от центра распределения, называются выбросами и экстремальными значениями, если они удовлетворяют определенным условиям.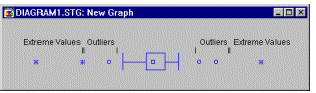

Точка будет экстремальной, если для ее значения выполнено следующее:

значение > ВЗП + 2*к.в.*(ВЗП-НЗП)
или
значение < НЗП - 2*к.в.*(ВЗП-НЗП)

где
ВЗП    верхнее значение прямоугольника на диаграмме размаха (например, среднее + стандартная ошибка или 75-процентиль).
НЗП    нижнее значение прямоугольника на диаграмме размаха (например, среднее - стандартная ошибка или 75-процентиль).
к.в.      коэффициент выбросов (если он равен 1.5, то экстремальные значения находятся на расстоянии, большем утроенной разности верхнего и нижнего значений прямоугольника).

Например, следующая диаграмма иллюстрирует выбросы и экстремальные значения на классической диаграмме размаха (за дополнительной информацией о диаграммах размаха см. Tukey, 1977).

Эксцесс. Эксцесс (термин был впервые введен Пирсоном, 1905) или точнее, коэффициент эксцесса измеряет "пикообразность" распределения. Если эксцесс значимо отличен от 0, то функция плотности либо имеет более закругленный , либо более острый пик, чем пик плотности нормального распределения. Функция плотности нормального распределения имеет эксцесс равный 0. Оценка эксцесса (выборочный эксцесс) вычисляется по формуле:

Эксцесс = [n*(n+1)*M₄ - 3*M₂*M₂*(n-1)]/[(n-1)*(n-2)*(n-3)*⁴]

где
M_j    равен (x_i-Mean_x)^j
 n      - число наблюдений
⁴     - стандартное отклонение (сигма), возведенное в четвертую степень.

См. также Описательные статистики.

Эллипс для предсказанного интервала (области) и эллипс размаха.
Эллипс для предсказанного интервала (области): Эллипс такого типа используется для обозначения доверительного интервала для предсказанных значений единичного наблюдения (предсказанного интервала). Такие двумерные доверительные или контрольные границы используются, например, на многомерных контрольных картах при промышленном контроле качества (см. работу Montgomery, 1996; а также раздел Карты T-квадрат Хотеллинга).

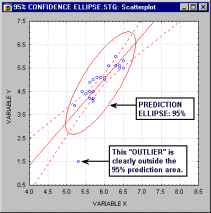
Параметры этого эллипса вычисляются в предположении о том, что две переменные имеют двумерное нормальное распределение. Ориентация эллипса определяется знаком линейной корреляции между двумя переменными (более длинная ось эллипса накладывается на линию регрессии). Вероятность того, что новые значения пары переменных (x и y) попадут в область, ограниченную эллипсом, равна значению коэффициента, задающего эллипс (например, 95%). Дополнительную информацию можно найти в работах Tracy, Young, and Mason (1992) или Montgomery (1996); см. также описание эллипса для предсказанного интервала.
Эллипс размаха: Эллипс такого типа имеет фиксированный размер, определяемый следующим образом: длина его горизонтальной и вертикальной проекций на оси X и Y (соответственно) равна среднему значению величины (Размах * I), где среднее и размах относятся к переменной X или Y, а I - текущее значение коэффициента.

Эпоха (для нейронных сетей). В итерационном обучении нейронной сети - один проход по всему обучающему множеству с последующей проверкой на контрольном множестве.

Подробнее см. в разделе Нейронные сети.