La troisième Loi de Kepler permet de connaître les dimensions du système solaire en unités relatives, par exemple en "unités astronomiques" (UA), où 1 UA est la distance moyenne du Soleil à la Terre. Cependant exprimer l'UA en kilomètres ou en milles nécessite l'utilisation d'une certaine variété de parallaxe--la petite différence des positions relevées pour un objet du système solaire, s'il est observé depuis deux points différents dont la distance qui les sépare est connue (en kilomètres ou milles). Les objets planétaires étant considérablement éloignés, le problème est que la différence de leur position apparente, vue depuis deux endroits éloignés de la terre, est tout à fait infime. Edmond Halley a suggéré d'utiliser le passage de Venus devant le disque du soleil : elle apparaît alors comme une tache ronde foncée -- ou pour citer un observateur du passage de 2004, "comme une myrtille devant une orange." C'est un événement relativement rare. Les passages se produisent par paires sur plus d'un siècle d'intervalle : aucun passage n'a eu lieu au XXéme siècle, il y en a eu un le 8 juin 2004, qui sera suivi d'un nouveau en 2008.
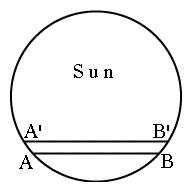
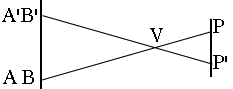
Supposez qu'un observateur situé au point P sur la terre observe la traversée de Venus devant le disque du soleil, de A à B (schéma 2 ci-dessus --deux figures, de face et de profil). Le mouvement apparent de Venus à travers le disque du soleil résulte des mouvements orbitaux combinés des deux planètes. Plus une planète est proche du soleil , plus elle se déplace rapidement, en vertu des lois de Kepler : Venus se déplace en conséquence plus rapidement que la terre, et la rattrape fondamentalement lors de son passage. Le plan de l'orbite de Venus est tout à fait proche de celui de la terre, connu habituellement sous le nom de plan de l'écliptique (proche, mais non identique -- sinon un passage se produirait chaque fois que Venus rattraperait la terre). Sur la sphère céleste la ligne AB est par conséquent presque parallèle à la ligne de l'écliptique qui est la ligne d'intersection du plan de l'écliptique à la sphère céleste, de notre point de vue du ciel. Observée d'un point différent P', Venus se déplace selon A'B', pratiquement parallèle à AB . Cet autre point est situé idéalement de l'autre coté de l'équateur, c'est à dire en outre de l'autre côté de l'écliptique. Si nous mesurons alors la distance D entre AB et A'B', nous pouvons en principe appliquer à la parallaxe une trigonométrie simple et calculer la distance PV entre P et la position V de Venus. Si seulement l'astronomie étaient si facile ! En fait, les lignes AB et A'B 'sont extrêmement proches l'une de l'autre. La figure du haut de la page (dont la source est ici) montre les images de Venus devant le soleil, obtenues le 8 juin 2004, depuis 3 emplacements, avec leurs données marquées de couleurs différentes. A l'évidence les tracés sont très rapprochés, à moins d'un rayon de Venus. La mesure séparées de chacune de ces données et le calcul de leur séparation D n'est pas susceptible de donner un résultat très précis. Ceci fait que Halley fit connaître qu'une information équivalente pouvait être obtenue en chronométrant les passages de Venus de A à B et de A' à B'. En effet le bord ("limbe") du soleil étant courbe, la longueur AB diffère de celle de celle de A' B' (nous disons "longueur" par convenance - en fait AB, A'B 'et D sont des angles apparents). La vitesse apparente du mouvement de Venus lors de sa traversée du soleil reste presque identique pour tout point de la terre, et donc évaluer la différence des temps entre les parcours AB et A'B ' permet de calculer la distance D. C'est beaucoup plus précis parce que le passage dure plusieurs heures, et que la différence du temps de transit peut s'élever à quelques minutes. De tels laps de temps peuvent (en principe) être mesurés tout à fait exactement. Dans ces sections nous décrirons une procédure simplifiée de calcul de l'unité astronomique en utilisant les temps de passage prévus pour le 8 juin 2004. Les astronomes qui ont établi ces durées -- disponibles ici sur le web--recourent naturellement à la valeur bien établie de l'unité astronomique : ici, ce n'est qu'un simple exercice. Si il s'agissait d'un "vrai" calcul, les valeurs observées auraient été adoptées.Ce sera un calcul assez approximatif, usant de simplifications et négligeant des corrections nécessaires aux déterminations réelles. Puisque nous nous sommes donné la liberté de choisir les stations d'observation, nous en choisirons deux de même ( presque ) longitude et latitude nord et sud égales de part et d'autres de l'équateur. Elles se situent tous deux en Afrique. (latitude et longitude à moins d'une moitié de degré)
Cette symétrie des positions simplifie l'analyse. Comme il a déjà été signalé, le mouvement apparent de Venus devant le soleil est presque entièrement dû aux déplacements de la terre et de Venus sur leurs orbites. Puisque la terre parcours son orbite à 30 km/s, on peut penser que la contribution à la vitesse due à la rotation de la terre peut être négligée, puisqu'elle n'atteint que 100 mètres/seconde. Mais cette vitesse déplace l'observateur durant la totalité de la durée du passage, pendant plus de 5 heures. Pour certains observateurs c'est presque un rayon terrestre, et la différence du déplacement entre les observateurs selon les différentes latitudes peut atteindre plusieurs milliers de kilomètres. Par ailleurs, le calcul de l'unité astronomique est obtenue sur la base d'une différence de temps ΔT n'égalant qu'environ 5 minutes, durant lesquels la terre se déplace d'environ :
Si la distance des deux points comporte une différence asymétrique additionnelle de quelques 1000 kilomètres, cela peut sérieusement dégrader le résultat, et demande une correction supplémentaire. Ici, nous évitons donc ce problème et simplifions le calcul en choisissant deux emplacements symétriquement distants de l'équateur, et donc de vitesse de rotation égales. Le choix d'une longitude presque commune égalise également les vitesses par rapport à Venus et au soleil. Ainsi les deux transits sont presque également équivalent, et nous n'apporteront pas de correction supplémentaire à ΔT . Cette page Web est en relation avec les deux suivantes La prochaine montre le calcul de D. Celui ci se réfère à une partie de la trigonométrie expliquée dans le "rafraîchissement de maths" et en particulier les formules des sommes de sinus et de cosinus, vues dans la section M-11. La page suivante établit la valeur approximative de de l'unité astronomique. En raison des approximations utilisées, le résultat n'est exact qu'à quelques pour cent prés, mais n'exige que de passer par les outils mathématiques envisagés ici. Elle donne aussi un aperçu de certains problèmes que doivent résoudre les astronomes Archives de photo du passage (dont une coïncidant avec un avion en vol). Pour une vaste collection de liens sur le passage de Venus, cliquez ici |
![[IMAGE: Image of Venus Transit]](Sfigs/Venus2.gif)