TPS-lidar.

A telescope can be used to observe particles and to measure their size (over 1"). Suppose, you have a pulse lidar with one transmitting and one receiving channel (one-position scheme lidar - OPS lidar, see Fig. p1).

Figure p1. Model of OPS lidar.

Then the delay time between a start pulse of the lidar and its reflection from the cloud can be used to determine distance to the cloud (see the first peak in Fig. p3) Having at your disposal information on the distance and particle angular size, you can determine particle cross-size. It is obvious, that the shorter distance to the cloud, the smaller particles you can observe.

Suppose you have at your disposal only a lidar with one receiving and two transmitting channels (TPS lidar - two-position scheme lidar, see Fig. p2).

Figure p2. Model of TPS lidar.

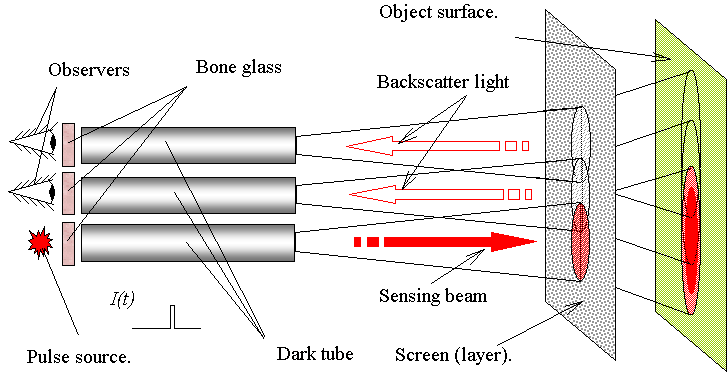
Through receiving channels of the TPS lidar an observer cannot see the subject outline, since he looks through a bone (scattering) glass. However, it will suffice to receive signals from a subject located behind the cloud within the field of view of the receiving channels in order to determine particle size (see Fig. p3).

Figure p3. Time diagram of backscattering signal. The first peak is backscattering signal form cloud particles. The second peak is backscattering signal from a test-object surface.

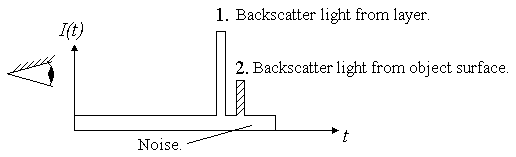
In this case it turns out that the far the cloud is from the TPS lidar, the smaller particles you can determine. TPS lidar angular resolution can be much higher than that of a telescope.

II. Annotation.

Our goal is to develop a method to determine by remote sensing surface density and cross size of opaque spots (cells, disks) located on a transparent screen, which absorbs and distorts light beams as an investigated medium. A sensing beam passing through such a screen generates a diffuse halo. It is shown that data provided by TPS lidars make it possible to determine halo angular size and screen absorption coefficient. These coefficients are sufficient to solve our task. Generally this method can be applied to restore dimensions and concentration of particles in a layer or in a scattering medium. Hereinafter by basic microphysics parameters we understand cell size and surface density of spots on a screen, as well as particle size and concentration in a medium.

III. Introduction.

At present the OPS lidar is the simplest device for remote sensing [1]. The OPS lidar calibration lies in receiving a signal from a subject with known angular dependant dispersion. Surfaces scattering according to Lambert law as well as medium consisting of particles with known scattering parameters can be considered among such subjects. It is a complicated experimental problem to create such objects and carry out the lidar calibration. A set of coefficients, received as a result of calibration, makes it possible to determine trace dependence of the backscattering coefficient with the use of the signal time dynamics. Backscattering coefficient depends on two basic microphysical parameters of the medium.

Extinction coefficient, which also depends on two basic microphysical parameters of the medium, can be measured on traces limited by the object surface. Therefore backscattering and extinction coefficients cannot be considered as indicators of any of basic microphysical parameters.

Remark 1. In some cases ratio of backscattering coefficient to extinction coefficient depends on particle size. Such cases present no practical interest since they either require a large volume of a priory information on the scattering object or are unique.

Existing methods (see, for instance, [2]) utilize data from OPS lidars received at several wavelengths. However, when determining, based on this information, microphysical parameters of the medium (see below), we encounter an ill-posed inversion problem. To solve this problem we need a priory information (known in advance) about scattering medium (for instance, real and imaginary parts of the material (of particles) refraction index, particle size distribution shape, etc.) since otherwise solution of the problem will not be the only one. Let us note essential disadvantages of such methods:

There is no obvious indicator of particle size

There are no conditions to adjust the lidar for the expected particle size

Reliability of determined particle parameters presents a problem.

A full set of real aerosol microphysical parameters such as particle size distribution shape, optical properties of the particle material, etc. almost always exceeds that of parameters measured with the use of remote sensing methods in number of its components.

A way out of the impasse is connected with another approach which goal is determined in Annotation. An instrumental method (IM) to determine by remote sensing basic microphysical parameters of the scattering medium has been developed on the basis of this approach. This method has the following characteristics:

IM1 - parameters or their combination to be measured must depend only on one of basic microphysical parameters of the medium
IM2 - for a specified experimental geometry there are particles with size variations corresponding to the max measurement accuracy
IM3 - there is a method to calculate inaccuracy of basic microphysical parameters of the scattering object.

If condition IM1 is satisfied, it means that there are some calibration methods available. Condition IM2 implies availability of an optimal range of basic microphysical parameters for a specified experimental geometry. Condition IM3 excludes an ill-posed inversion problem when interpreting data received in the course of sensing.

The proposed method can be applied, in particular, for solar system planet atmosphere investigation, since it requires a min volume of a priory information on the scattering medium, see chapter Some philosophy.

IV. Detailed Picture.

§1. Ideal scheme of sensing & random transmission screen.

IS model

Figure 1.1 Ideal scheme (IS). RTS (random transmission screen), test-object.

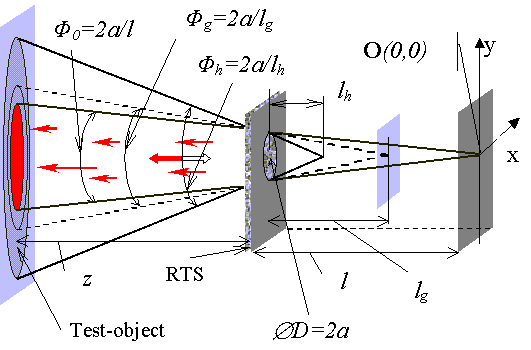
Ideal scheme (IS) of remote sensing is scheme in the Fig. 1.1. Field of view and beam geometry are described by the same function. This scheme was discussed in Fresnell approximation (Small angles) [А9].

Receiving point and point light source are mounted at the point О(0,0). Light beam and field of view are formed by a hole. The hole has Gaussian transmission function

M=M₀ exp(-r²/4a²), (1.1)

r(x,y) is coordinate vector in the whole plane, а radius of the hole, M₀ – transmission in the center of the hole. Optical axes of the receiving and transmitting channels coincide. The observation plane with point О(0,0) on it, lies at the distance l from the hole (see Fig. 1.1). Test-object surface lies at the distance z from whole plane (see Fig. 1.1).

Fields of view and beam geometry are described one point spread function. Radial intensity distribution in the test-object is Gaussian. Diffraction distortion is minimum due to soft boundary of the hole. Beam angular size Ф₀ is formed by the one hole and is equal to 2а/l (see Fig. 1.1). Angular size Ф₀ is measured from observation plane in geometrical optic.

Trace dependence of backscatter intensity in geometrical optic approximation l/l_d<<1, l_d=2ka², where k – wave number, is given as (see [А9])

I(z)/I₀=(1+z/l)^-2. (1.2)

Parameters z, l are introduced upper, I(z) is backscatter signal in the point O from test-object for distance z, if z=0 then I(z)=I₀. Longitudinal size l is equal to remote scale of signal decrease (see Fig. 1.1).

Time dependence of the backscatter signal is described by (1.2) for delta function impulse and substitution z=ct/2, c is light speed, t is travel time (time delay between start pulse of light and received signal of backscatter light). Henceforth the signal in the point O is considered as maximum amplitude of backscatter intensity from test-object surface (see second peak in the figure p3).

Other dependence instead of (1.1) is used in lidar equation always (see Appendix 1).

Let a random transmitting screen (RTS) is mounted in the whole plane (see Fig. 1.2).

Figure 1.2 Random transmitting screen (RTS).

Round opaque cells (disks) of diameter d_c produce random transmission. Surface density of these cells is n_c. RTS yields two effects:

1. Absorption. Absorption probability q=1-р, р is transmission probability. Henceforth the following estimation q=(1-р)<<1 is valid (transmission probability is small). In this case opaque cells scatter sensing beam independently.

2. Beam distortion . Diffuse halo around of beam is produced because of diffraction in opaque cells. Let the halo angular size be small (Fresnell approximation is valid).

Transmission probability is considered р as ratio beam intensity crossing RTS to beam intensity before RTS.

The trace dependence of backscatter signal from test-object I_s(z) decreases more quickly if RTS is mounted than without RTS because of increase of beam angular size. As results the expression (1.2) is modified as (see [А8] also):

I_s(z)/I₀=p² /(1+z/l_g )² . (1.3)

Parameters p, z are introduced upper, I₀ is backscatter intensity of signal without RTS for z=0, parameter l_g: l_g<l simulates trace dependence of signal decrease if RTS is mounted. Beam angular increase can be simulated by decrease of longitudinal size of IS from l to l_g<l (see Fig. (1.1)).

Remark 2. The expression (1.3) is valid if the distance z lies in Fraunhofer zone. Otherwise (RTS is mounted in the whole plane) measured backscatter signal is proportional the first index of power of transmission probability p.

Measurement of parameters p and l_g by IS model

Let parameter l and beam angular size Ф₀ are known. Determination of parameters p and l_g by IS model consists of the following steps:

St1. Parameter l_g is measured from trace dependence of backscatter signal if RTS is mounted (see Appendix 2).

St2. Transmission probability p is measured by ratio of backscatter signals in cases RTS is mounted and without RTS from (1.2) and (1.3) as

p=(I_s(z)/I₀)^1/2(1+z/l_g)(1+z/l)^-1 . (1.4)

Parameters I_s(z), I₀, z, l, l_g are introduced upper.

Simulation of beam distortion

The beam distortion is a sum of the undistorted part of beam and the diffuse halo part (see [А8]) as

(1+z/l_g)^-2=p²(1+z/l)^-2+(1-p²)(1+z/l_h)^-2 . (1.5)

Parameters z, l_g, p, l are introduced upper, parameter l_h simulates of signal decrease along of sensing trace for beam with halo angular size. Model IS with longitudinal size l_h gives beam with halo angular size (see Fig. 1.1). Angles Ф_g and Ф_h are described via l_g and l_h as

Φ_g=Φ₀l/l_g, Φ_h=Φ₀l/l_h . (1.6)

Parameters Φ₀, l, l_g, l_h are introduced upper.

Halo angular size can be found from equation (1.5) because it has one unknown parameter l_h. Method of measurement l_h is supposed in paragraph 2.

An expression (1.5) to discuss

We have the following cases:

- p=1 and l=l_h=l_g and (1.5) is valid. There is no RTS.

- p<1 and l=l_h=l_g. Halo angular size is equal to beam angular size Φ_h=Φ₀. It means large size of cells of RTS. As a result the diffraction angle is far less than beam angular size. The expression (1.5) is valid.

- RTS is substituted by random phase screen and absorption probability is equal to zero then the expression (1.5) isn't valid because the beam does not have any undistorted part. The expression (1.5) can be used if the following condition is valid:

I_s(z)/I₀<(1+z/l)²(1+z/l_g)^-2 (1.7)

Parameters z, l, l_g are introduced upper. If (1.7) is valid then investigated screen (for example RTS + Phase screen) has RTS equivalent. Condition (1.7) cannot be valid in the following cases:

l_g

B. Phase distortions of sensing beam exist (for example, special variations of refraction index).

- p<<1 and l_h=l_g (Absorption probability is large). Halo angular size is equal to beam angular size Φ_h=Φ_g, because undistorted part of beam in the test-object surface is small. The following condition is valid (instead of (1.7))

I_s(z)/I₀<<(1+z/l)²(1+z/l_g)^-2 (1.8)

In this case halo angular size depends on distance between opaque cells for RTS. If RTS is replaced by it's negative (holes are randomly distributed in opaque screen instead of opaque cells) then the expression (1.5) is valid because the first addend mach less of the second addend. Hence the expression (1.5) is valid again.

Φ_h as halo angular size

The first addend in (1.5) is undistorted part of signal intensity crossing via RTS for double path. The second addend is intensity of waves are scattered by boundary opaque cells RTS. Hence the expression (1.5) is development of conception for boundary diffraction wave are produced halo (see [3] and Appendix 3). Angular size Φ_g for RTS is equal to angular size for it's negative because concept of boundary diffraction wave is valid in both cases. According to Babinet principle the sum fields for RTS and it's negative does not give halo.

Other method exists for diffuse halo description. Absorption probability q=1-p in (1.5) can be substituted for extinction probability q_e: q_e>q (see Appendix 4). Halo angular size is defined by absorption coefficient is not equal to halo angular size defined by extinction coefficient. Hence real halo angular size in the test-object surface could not be equal to measurable Φ_h. However, for both cases parameter Φ_h can be used as parameter halo angular size.

For some cases parameter l_g (see Appendix 5) can be used for halo angular size.

Basic microphysical parameters of RTS

Opaque cells of RTS scatter beam independently. Hence if surface density increases then halo intensity increase but halo angular size does not change. If size of cells increases then halo angular size decrease because of decrease of diffraction angle for cells. Hence angle parameter Φ_h is indicator of cells size of RTS.

The following problem is to define dependence between halo angular size from the sensing beam with angular size Φ₀ and Φ₀=0 (plane wave). If cells size of RTS decreases then halo angular size increases. If cells size increases then halo angular size tends to beam angular size. Hence angle Φ_h can be described via scattering angle for plane wave Φ_sp as (see also [А8])

Φ_h²=Φ₀²+Φ_sp², hence Φ_sp=[Φ_h²-Φ₀²]^1/2 . (1.9)

Parameters Φ_h, Φ₀ are introduced upper. Therefore if cells size is large (Φ_sp<<Φ₀), then Φ_h=Φ₀. If cells size is small (Φ_sp>>Φ₀), then Φ_h=Φ_sp. If radial distribution of negative in opaque cells of RTS is Gaussian then Gaussian distribution describes both beam geometry and halo. In this case the expression (1.9) is a result of Gaussian distribution properties. If opaque cells of RTS have hard boundary then measured scattering angular size for plane wave (1.9) Φ_sp is proportional to real angular size for plane wave with some proportional coefficient. This coefficient depends slowly on cells size and radial negative distribution in cells (see [A8]).

Angle Φ_sp=Φ₀ can be selected as optimal angle for measurements. In this case Φ_h=1.4 Φ₀. If Φ_sp>> Φ₀ then Φ_h=Φ_sp и z/l_h>>z/l. The second addend in (1.5) is far less then the first addend and error of definition Φ_h stay large. If Φ_sp<<Φ₀ then Φ_h is equal to Φ₀ approximately and error of definition Φ_sp from (1.9) will increase also.

Cells size d_c and surface density n_c for RTS are functions of measured parameters Φ_sp and р by means of С₃ и С₄ as

d_c=C₃λ/Φ_sp, и n_c=C₄(1-p)/d_c² . (1.10)

Here p, d_c, n_c are parameters introduced upper for RTS, λ is wavelength, C₃ and C₄ are calibration coefficients. Coefficients C₃ и C₄ can be measured by means of microphysical calibration with the use of standard RTS. This screen must be have known surface density and cells size.

Intermediate calibration coefficients (see [A8] and Appendix 6) can exist С₁ (An indicator of Fresnell approximation) и С₂ (An indicator of a periodic arrangement of the cells in the RTS).

Optimal interval of cells size for measurement is located near d_op=λ/Φ₀. If cells size d_c>>d_op then halo angular size Φ_h is equal to beam angular size approximately Φ₀ and as a result the angle Φ_sp obtained from (1.9) has large error. If cells size d_op>>d_c then the second addend in (1.5) is far less than the first addend (because of l>>l_h) and error of halo angular size Φ_h increase.

For RTS with different cells size the first expression in (1.10) for d_c gives effective cells size and the second addend for n_c gives effective surface density of number of cells in RTS.

§2. Two position scheme (TPS(2)).

Disadvantages of OPS

To measure of parameters l_g and p by OPS the following conditions must be realized

c1. Angle of incidence of sensing beam in test-object surface must not be changed for each distance

c2. Scattering properties of test-object surface must be homogeneous and must not be changed for the measurement duration

c3. Beam must be located within test-object surface.

The basic problem is the first condition c1, because length of trace to be sensed can be ranged from one hundred meters to several kilometers. Condition c1 presents a problem for calibration of OPS-lidars.

Condition c1 and conditions c2, c3 can be resolved with the use of the second receiving channel in IS.

Model of TPS(2)

Figure 2.1 Two-position scheme with two optical axes (TPS(2)).

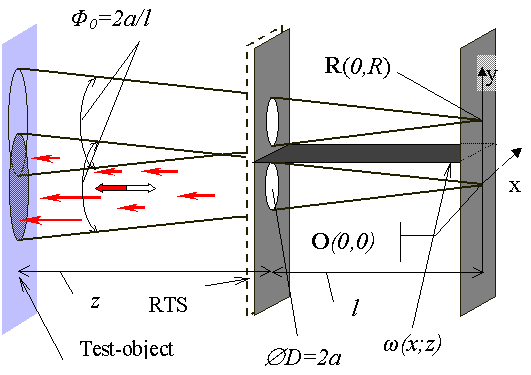
TPS(2) with two optical axes (TPS(2)) is considered in [А6]. The lower part of the TPS(2) (see Fig. 2.1) is IS. Upper part is additional receiving channel. IS and the additional receiving channel are insulated by the dark opaque screen ω(x;z). Distance between optical axes R is large R>>2a. In this case dark opaque screen ω(x;z) does not distort beam geometry and fields of view. Transmission function (1.1) is described the both holes. Observation plane is mounted at the distance l from the holes. This parameter describes trace decrease of signal (see Fig 2.1). Test-object surface locates at the distance z from the holes (see Fig. 2.1).

Geometrical form factor

Henceforth the ratio of backscattering signals Π(R;z/l)=I(R)/I(O) as the function of distance z we shall name by Local Calibration (LC) for TPS(2). To obtain LC data the condition c1 is not required, because angle between test-object surface and sensing beam can be changed for each distances z.

Intensities ratio for holes with Gaussian transmission function (1.1) in geometrical optic approximation (LC data) is equal to [А6]

Π(R;z/l)=I(R)/I(0)=exp(-R²/{4a²(1+z/l)²}). (2.1)

Parameters a, z, l, R, I(0)=I(0,z) are introduced upper, I(R) is a signal in the point R. LC data as a function of the distance represent a normalized two-dimensional convolution of point spread function for basic and additional channels or geometrical form factor [1]. According to definition the geometrical form factor is overlap function of the field of view for the additional receiving channel and the sensing beam. If the distance z increases then the overlap function increases too and the geometrical form factor increases (it's limit is equal to 1). If R=0 then the field of view and the sensing beam coincide as a result the geometrical form factor is equal to 1 for each distance (IS). The overlap function between field of view and the sensing beam exists always for holes with hard boundary and if Fresnell approximation is not valid.

Measurement of parameters p и l_g by TPS(2)

According to (2.1) the trace dependence of the signal decrease without RTS

I(R;z/l) = I₀Π(R;z/l)/(1+z/l)². (2.2)

Parameters I(R;z/l), I₀, Π(R;z/l), z, l are introduced upper. If R=0 then the trace dependence of the backscattering signal is defined by (1.2).

Let RTS be mounted in the whole plane of TPS(2). Halo is formed around of beam. The signal decreases more quickly for IS. This dependence can be simulated by means of decrease of the longitudinal size l to l_g <l in the equation (1.2). The backscatter signal I(R;z/l) and ratio of the signals Π(R;z/l) depend on nondimensional parameter 1+z/l without RTS. If RTS is mounted then ratio of the signals depends on 1+z/l_g.

Hence if RTS is mounted then the beam angular size and fields of view increase and the geometrical form factor increases too. On the other hand if the angular size and fields of view increase then the signal decreases more quickly along the path. Therefore parameter l_g can be measured with the use of the geometrical form factor only.

If RTS is mounted then the signals ratio increases before Π(R;z/l_g). New distance z_g is defined from LC data (see [A6] also) as

Π(R;z/l_g )=Π(R;z_g /l) . (2.3)

Here z_g is the distance obtained from the new intensity ratio Π(R;z/l_g). If l_g<l then Π(R;z/l_g)>Π(R;z/l), hence z_g>z.

Determination of parameter l_g with the use of LC data is presented in the figure 2.2. R=8a for TPS(2).

Figure 2.2 Determination of parameter l_g with the use of TPS(2).

Example e2.1 Symbols z, l, R, Π(R;z), z_g, l_g are used.

The curve 1 presents LC data for TPS(2) with l. Let the distance z=3l and Π(R;z=3l)=0.368. Let the RTS be mounted in the whole plane (see Appendix 2). Intensities ratio Π_s(R;z/l) increases up to 0.492, curve 1 yields distance z_g =3.75l for new intensities ratio Π(R;z_g/l ). We have the following proportion l_g/l=z/z_g=0.8. Hence z_g is the distance measured by means of LC data.

Therefore the parameter l_g is measured from the signals ratio (LC data) for TPS(2). Calibration is based on LC data is independent of the angle between the sensing beam and the test-object surface. Difference topographical objects for this calibration can represent this surface. Parameter l_g for IS is determined by the trace dependence of backscatter signal (see St1 and Appendix 2).

Transmission probability р is given by equation (1.4) with the use of LC data as

p=(I_s(z)/I₀)^1/2(1+z_g/l)(1+z/l)^-1. (2.4)

Parameters p, I_s(z), I₀, l, z_g, z are introduced upper.

Determination of the halo angular size Φ_h

Equation (2.3) is applicable for the halo angular size determination also with the use of proportion z_h/l=z/l_h. Then equation (1.5) is rewritten as

(1+Z_g)^-2=p²(1+Z)^-2+(1-p²)(1+Z_h)^-2 . (2.5)

Big letters Z_g, Z, Z_h denote relations z_g/l, z/l, z_h/l. Unknown parameter is Z_h.

If parameters Z_g and p are known then the distance Z_h is determined from (2.5) as

Z_h={(1-p²)/[(1+Z_g)^-2-p²(1+Z)^-2]}^1/2-1 . (2.6)

The halo angular size is given via Z_h as

Φ_h=g_hΦ₀=Φ₀Z_h/Z and g_h=z_h/z=Z_h/Z . (2.7)

Parameters p, Z_g, Z, Φ_h, Φ₀, z_h, z are introduced upper, g_h is coefficient of the halo angular size.

Therefore LC data determine transmission probability of RTS and the halo angular size.

Example 2.2. Symbols Φ₀, λ, S, d_op, С₁, С₂, С₃,С₄, z_g, z_h, Φ_h, Φ_sp, d_c, n_c are used.

We present typical of the transmitting and receiving channels of a lidar: Φ₀=1 mrad, λ=0.5 μm, aperture area is equal to S=πa²=10 cm². Hence d_op=λ/Φ₀=0.5 mm. As an estimate, we accept that С₁=С₂=С₃=С₄=1. The remote scale for TPS(2) is l=150 m; the distance between TPS(2) and the object surface is equal to 300 m.

Let the light scattered by object surface yields in the basic receiving channel N(R_m=0)=10⁶ and N(R_m=0)=0.6 10⁶ photocounts without and with RTS respectively. The distance z_g measured from LC data is 360 m. Condition (1.7) is valid. Eq. (2.4) yields transmission probability р=0.88. From Eq. (2.6), we find that z_h=3000 m; in this case, the error in the parameters z_g, p, N₀ should be near 0.1%. The equation (1.9) yields Φ_h=Φ_sp=10Φ₀. Equations (1.10) yield d_c=50 μm and n_c=4800 cells/cm². Hence the number of cells in the aperture area is 4.8 10⁴.

§3. Two position scheme & scattering medium.

The case of far screen

Figure 3.1

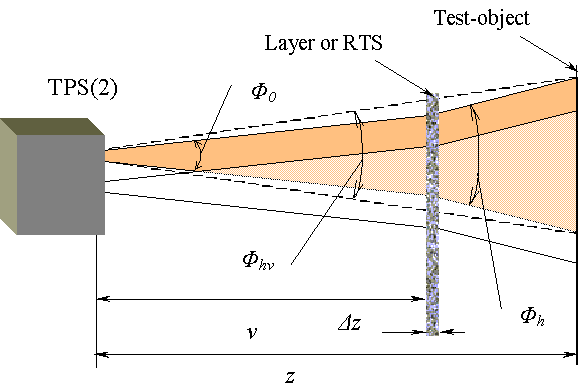
Let RTS be placed at the distance v (variable) from the whole plane of TPS(2) (see figure 3.1). If Z_h substituted by Z_hv then the equation (2.5) is valid also. (see [А9]). However the halo angular size Φ_hv measured by means of TPS(2) depends on the distance v and is given as (see (2.7))

Φ_hv= Φ₀·Z_hv/Z= Φ₀· z_hv/z. (3.1)

Here Φ₀ is the beam angular size, z is the distance between TPS(2) and the test-object surface (see Fig. 3.1), Z is nondimensional distance, parameters Z_hv=z_hv/l, z_hv, Φ_hv depend on the distance v (see Fig. 3.1). To determine the halo angular size Φ_h for v=0 the following expression is valid

Φ_h=g_hΦ₀=Φ₀ (Z_hv-V)/(Z-V)=Φ₀ (z_hv-v)/(z-v), V=v/l. (3.2)

Parameters Φ_h, g_h, Φ₀, Z_hv, l, Z, z_hv, v, z are introduced upper. If v=0 then a scheme in the fig. 2.1 is valid and v=0, z_h=z. If v tends to z then RTS is mounted on the test-object surface and measurement of the halo angular size is impossible. If 0<v<z then LC data and parameter l are enough for determination of Φ_h and p.

Let RTS is mounted at the distance v, test-object at the distance z and h << z , v, h=z-v (RTS is mounted near test-object). The optimal halo angular size Φ_hv be equal to 1.4Φ₀. Then the following estimation is valid (see (3.2))

Φ_h= (Φ_hv-Φ₀) v / h= 0.4Φ₀ v / h >> Φ₀ (3.3)

Parameters Φ₀, Φ_h, v are introduced upper. Increase the distance v (see Fig. 3.1) yields increase of the optimal halo angular size Φ_h. Hence the optimal diameter of cells decreases.

Example 3.1 The following symbols v, z, Φ_hv, Φ₀, Φ_h are used.

Let the distance v =0.95z, Φ_hv=1.4 Φ₀. Then h=0.05z and expression (3.2) yields Φ_h=9Φ₀ and Φ_sp=9Φ₀. It means d_c =λ/9Φ₀ (if the optimal diameter of disks on RTS for v=0 is equal to 1 mm then the optimal diameter of disks be equal to 0.1 mm for displacement of RTS at the distance v =0.95z). Hence the following estimation d_c<<λ/Φ₀ for the size of opaque cells can be valid.

TPS-lidar & telescope

Data from example 3.1 are used for comparison of TPS-lidar and telescope.

Angular resolution of a big telescope is equal to 1'' second of arc. This is accuracy of angular measurement of stars. Hence the diameter of cells 0.5 mm at the distance 100 m can be observed via the telescope.

Let the transmitting channel of TPS(2) has impulse source with the wavelength 1 μm. If the distance from the test-object z=100 m and the distance v=95 m then the optimal measurable diameter of cells is equal to 100 μm. It means 0.1'' second of arc for the angular resolution. If the distance z=1000 m v=995 m then the optimal measurable diameter of cells is equal to 10 m. It means 0.001''second of arc for the angular resolution.

Changing of RTS by layer

Let opaque cells of RTS are substituted by dark spheres (complex refractive index is large) with diameter d_s >>λ. Then cross-section for sphere is equal to cross-section for opaque cell of diameter d_s. This cross-section is equal to 2σ where σ is geometrical section of particle (sphere or cell) (see [5] also). Let spheres is random distributed in a layer with thickness Δz and optical depth τ. Then the following substitution is valid

p=exp(-τ) , где τ= kz , (3.4)

and equation (2.5) is rewritten as

(1+Z_g)^-2=exp(-2τ)(1+Z)^-2+(1-exp(-2τ))(1+Z_hv)^-2. (3.5)

Parameters p, Z_g, Z, Z_hv, z are introduced upper and k is absorption coefficient.

Remark 3. If RTS is substituted by a scattering layer then contributions of multiple scattering effects increase because of increase probability of a return of the scattering radiation back to the layer. As a result the measurable halo angular size for multiple scattering effects is bigger then for single scattering effects. However if the optical depth is small then multiple scattering effects are neglected. If the optical depth is not small then multiple scattering effects can be measured (see Appendix 7).

Instead of equations (2.4), (2.6), (2.7) we shall have the following equations for measurable parameters (see [A9] also):

τ=-0.5ln{(I_s(z)/I₀)^1/2(1+Z_g)(1+Z)^-1} , (3.6)

Z_hv={(1-exp(-2τ))/[(1+Z_g)^-2- exp(-2τ) (1+Z)^-2]}^1/2-1, (3.7)

Φ_h=g_hΦ₀=Φ₀ (Z_hv-V)/(Z-V)=Φ₀ (z_hv-v)/(z-v). (3.8)

Parameters τ, I_s(z), I₀, Z_g, Z, Φ_h, g_h,Φ₀, Z_hv, V, z_hv, v, z are introduced upper. Hence LC-data and l allow to measure parameters Φ_h and τ for the scattering layer.

Effective diameter d_s(scatter) and number concentration of spheres in the layer n_s are given as (see [A9] also)

d_s=C₃λ/Φ_sp and n_s=C₄τ/d_s²Δz (3.9)

Parameters C₃, λ, C₄, τ, Δz are introduced upper. Equations (3.9) yield basic microphysical parameters of the scattering layer because a type of scattering does not change if a sphere is substituted by disk with the diameter of sphere. It means the following estimation d_op <<λ/Φ₀ can be valid for the optimal particle size.

Scattering medium

Let a random homogeneous scattering medium between TPS(2) and test-object surface is formed only monodisperse scattering particles. A sequence of layers along the sensing trace z simulates halo from the scattering medium. Eq. (3.5) are rewritten as (see [A9] also)

(1+Z_g)^-2=exp(-2τ)(1+Z)^-2+(1-exp(-2τ))(1+Z_hM)^-2, (3.10)

distance Z_hM is given as

Z_hM=[(1-exp(-2τ))/γ]^1/2-1, where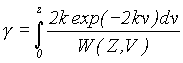

, W(Z,V)=[1+g_h(Z-V)+V]², (3.11)

g_hM=Z_hM/Z .

Parameters Z_g, τ, Z, v, g_h, V are introduced upper. Eq. (3.11) is obtained by total layer contributions between TPS(2) and test-object surface.

If g_h is the angular increase of a thin layer for V=0 then g_hM is angular increase for the medium between TPS(2) and the test-object. If τ<0.01 then dependence g_hM(g_h) is given as

g_hM={[(1+Z)(1+g_hZ)]^1/2-1}/Z. (3.12)

Parameters Z, g_h are introduced upper. Hence if g_h>>1 then the halo angular size from the scattering medium is g_h^1/2 times as scattering angle of one particle g_h. This result can be obtained from radiative transfer equation. According to this equation the halo angular size in the homogeneous scattering medium increases as z^1/2.

Example 3.2 Symbols Φ₀, λ, C₁, C₂, C₃, C₄, d_op, l, z, g_hM, z_g, n_s are used.

We use the following parameters from Example 2.2: Φ₀=1 mrad, λ=0.5 μm, C₃=C₄=C₁=C₂=1 and S=10 cm². Then d_op=λ/Φ₀=0.5 mm. The parameter l is equal to 150 m, the distance z=300 m. Let scattering centers be opaque spheres with diameter d_s=50 μm form the homogeneous medium along the sensing trace and d_s=50<< d_op. The optical depth τ=0.1. Eq. (3.12) yields g_hM=3.5 for the angle increase of halo for the homogeneous medium. Eq. (3.10) yields z_g=342 m. Eq. (3.9) yields n_s=1.6 particles/cm³.

Therefore the method of determination of microphysical parameters is based on calibrations of two categories

-1c- Local calibration determines of the absorption coefficient and the halo angular size.

-2c- Microphysical calibration determines of the effective size and the surface density of number of cells in RTS (the number concentration for a layer or the homogeneous medium).

Comparison of OPS and TPS(2)

Table 1.

TPS	OPS
Distance measurement
1. Time delay method (see the first peak in the Fig. р3). 2. Signals ratio method.	Time delay method (see the first peak in the Fig. р3).
Basic measurable parameters and calibration methods.
Backscatter coefficient, calibration methods are identical.
1. Absorption coefficient. 2. Halo angular size. Local calibration data LC.	1. Extinction coefficient. If beam geometry is undistorted, calibration is not required.
Determination of basic microphysical particle parameters.
Microphysical calibration.	Ill-posed inversion problem.

Conclusion

Basic parameters measured TPS(2) are transmission coefficient (1.4) and beam distortion angular size . Combination of these parameters determines halo angular size (see (1.5)). Halo angular size is indicator of particle size. If halo angular size increases then effective particle size decreases. If halo angular size decreases then effective particle size increases.

Particle size λ/Φ_h is optimal for measurement by TPS(2) (It is valid if v=0 see Fig. 3.1 ). If particle size decreases then halo angular size increases and the second addend in equation (3.5) stay much less of the first addend and error of halo angular size increases. If halo angular size decreases then expression (1.9) for calculation Φ_sp has neighbor angles. As a result error Φ_sp increases.

If distance between layer and TPS(2) increases then optimal particle size decreases.

Restored microphysical parameters scattering particles (see (1.10) and (3.9)) and errors determine effective RTS (effective medium). This RTS has opaque cells of one radius (monodispersal particle size for medium) and produces as transmission and distortion of the beam as the investigated medium.

Hence remote sensing instrumental method of measurement of microphysical parameters by means of TPS can be realized because it has characteristics IM1, IM2, IM3.

V. Some comments.

Description of the beam distortion in scattering medium by means of Radiative Transfer Equation is given in [6], [7]. These results are adequate to our conception. Angular moments of scattering indicatrix of one particle are required for description beam geometry in scattering medium. To calculate halo angular size we must know differential cross-section for one particle and particle size distribution. However these moments cannot exist even for small scattering angle (around disk with hard boundary, for example). Therefore necessary (but not enough) condition to use radiative transfer equation is the big volume a priory information about scattering medium. This information is excessive because volume concentration of number of particle and particle size are main information. This contradiction and deficit forward methods of measurement beam angular distortion are basic problem for application of remote sensing methods.

Some philosophy

As seen from the above, determined (restored) particles microphysical parameters can mismatch the existing medium. A priory information on the scattering object is required to prove their correspondence, namely diffuse halo must be generated only by statistical heterogeneities of the object, for instance, by particles. In this case determined (restored) microphysical parameters of the medium describe a model homogeneous object consisting of monodispersal scatters (opaque spheres have one diameter). Such a model presents a core of our vision of the object (Vorstellung) under examination and makes it possible to find out quantitatively the reason for the beam attenuation. Whether the attenuation is caused by increase in concentration or scatters size. An OPS lidar and telescope can be used to receive more detailed information on the medium, see Presentation. Observing particles through a telescope we can divide them into groups by their size, shape, color (single scattering albedo), etc. The result of observations is a (multidimensional) function of distribution in groups of parameters. It is clear that the second method is more preferable since it carries more information. Let the Lord make you patient to realize this method.

VI. Possible applications.

A1. Angular beam distortion measurement for screens with different phases. These measurements require only data on local calibrations. An experimental scheme is given in Fig. 2.1. Signals backscattered by the object surface with a screen and without it present parameters to be measured. Possible application:

- mirror and glass surfaces quality control (according to

Φ_g

) with the use of quantitative methods

A2. Determination of effective size and surface density of particles on mirror or transparent screens. These operations require data on local and microphysical calibrations. For such a scheme (see Fig. 2.1) parameters to be measured are signals backscattered by a test-object surface with or without a screen. Possible application:

- dust particles effective size and surface density measurement. Particle size is to be large enough

d>>λ

A3. Determination of particle effective size and concentration in a certain volume. These operations require data on local and microphysical calibrations. An experimental scheme is given in Fig. 3.1. Parameters to be measured are signals backscattered by a test-object surface with or without a cloud of scattering particles. Possible application:

-aerosol particle effective size and concentration measurements in rainy, snowy and foggy conditions

-particle effective size and concentration measurement in a city atmosphere and in tail areas.

P.S. There are other possible applications of local calibrations.

VII. References.

1. R. Measures. Laser Remote Sensing – fundamentals and applications. New York: John Wiley and Sons, (1983).

2. Veselovskii I., Kolgotin A., Griaznov V., Muler D., Wandinger U., Whiteman D. N., Inversion with regularization for the retrieval of tropospheric aerosol parameters from multiwavelength lidar sounding. Appl. Opt. 2002, Vol. 41, No. 18, 3685-3699.

3. M. Born and E. Wolf, Principles of Optics, 4^th ed. (Oxford and New York: Pergamon Press, 1970). For an account of the Rubinovicz theory (boundary diffraction wave), see Sec 8.9.720 с.

4. Meki K., Yamaguchi K., Sato X. L. Y., Kawahara T. D., Nomura A., Opt. Lett., 1996, 21, 1318.

5. H. C. Van de Hulst, Light Scattering by Small Particles, New York: Wiley, 1957.

6. A. Ishimaru, Wave Propagation and Scattering in Random Media, Vol. 2, Multiple Scattering, Turbulence, Rough Surface and Remote Sensing, Academic Press, New York, 1978.

7. Katsev I., Zege E. P., at al. J. Opt. Soc. of Amer. A, 1997, 14, 1338.

VIII. Some author’s references.

A1*. Bukharin A.V., Pershin S.M. Theoretical analysis of an eye-safe lidar, Atmospheric and Oceanic Optics, vol. 7, 1994, № 04, p.276.

A2*. Pershin S.M., Bukharin A.V., Linkin V.M., Makarov V.S., Calibration of an aerosol lidar operating in photon counting regime and detection of atmospheric inhomogeneities, Atmospheric and Oceanic Optics, vol. 7, 1994, № 04, p.284.

A3*. Pershin S.M., Bukharin A.V., Makarov V.S., Kuznetsov V.I., Prokhazka I., Spatiotemporal picture of the atmospheric pollution with aerosols over Volga River, Atmospheric and Oceanic Optics, vol. 7, 1994, № 04, p.290.

A4. Bukharin A. V., Measuring the extinction in scattering media by two-channel lidar, Physics of Vibrations, 2000, Vol. 8, Number 3, pp. 165-171.

A5. Bukharin A. V., Distance measurement with CW-source two-position sensing scheme, Physics of Vibrations, 2001, Vol. 9, Number 3, pp. 197 - 204.

A6. Bukharin A. V., Method for measurement of beam lateral distortions with two-position sensing schemes, Physics of Vibrations, 2001, Vol. 9, Number 4, pp. 246 - 255.

A7. Bukharin A. V., Local calibration principle as applied to determination of extinction coefficient in atmosphere by two-position sensing schemes, Physics of Vibrations, 2002, Vol. 10, Number 2, pp. 78 - 86.

A8. Bukharin A. V., Two-position scheme applied for determination of microphysical properties of random transmitting screen, Physics of Vibrations, 2002, Vol. 10, Number 3, pp. 177 - 184.

A9. Bukharin A. V., Two-position systems in remote determination of microphysical properties of scattering media, Physics of Vibrations, 2002, Vol. 10, Number 4, pp. 228 - 235.

* 1-3 papers about OPS – lidar.

IX. Appendixes.

Appendix 1. The following trace dependence instead of (1.2) is applicated for lidar always (see [1])

I(z)/I₀=A(z)O(z)/z², (a1.1)

Parameters I(z), z, I₀ are introduced upper, О(z) is geometrical form factor field of view and sensing beam, А(z) is effective aperture of the receiving channel. This dependence is used for nonideal scheme.

For IS О(z)=1 and (a1.1) is rewritten as

I(z)/I₀= A(z)/z². (a1.2)

Expressions (a1.1) and (a1.2) have not of the longitudinal size of signal decrease l. As a result this parameter is not used in lidar equation.

Appendix 2.

If RTS is mounted the signals ratio for two distance from test-object surface z₁, z₂ is equal to (taking into account for (1.3))

I_s(z₁)/I_s(z₂)=(1+z₂/l_g)²(1+z₁/l_g)^-2 (a2.1)

As a result parameter l_g is equal to

l_g =( z₁ (I_s(z₁)/I_s(z₂))^1/2- z₂) (1-(I_s(z₁)/I_s(z₂))^1/2)^-1 (a2.2)

Parameter l_g can not be measured always because angle between test-object surface and beam optical axis can change. However if l_g is known then transmission probability p can be determined (see (1.4)).

Appendix 3.

Let us consider observer in the test-object surface. Beam intensity distribution is a result of diffraction in the opaque cells of RTS. The field is sum of the geometrical undistorted part of beam and field from diffraction boundary wave (see [3]). Then intensity distribution of scattered beam in the test-object surface is equal to

I(z)=I₀[p(1+z/l)^-2+(1-p)(1+z/l_h)^-2] (a3.1)

Parameters I₀, p, z, l, l_h are introduced upper. The second addend in (a3.1) is shadow part of RTS. Hence only diffraction boundary waves determine the halo interpretation if absorption coefficient is used.

Let us consider observer in the point of the beam source. This scheme of measurement repeats the upper scheme if two RTS are mounted. Interpretation halo by means of the boundary diffraction waves is applicated in this case.

Appendix 4. Extinction probability is equal to ratio intensity undistorted beam output if RTS is mounted to beam intensity without RTS. Then according to Kirhhoff theory [3] halo is produced by the some area around of the opaque cell of RTS. Disadvatages of this interpretation is measurements undistorted part of beam for transmission probability q=1-p>0.5. However undistorted part of the beam can be measured by means of CCD camera (see [4]). Two images undistorted part of beam with and without RTS are enough for determination extinction probability.

Appendix 5.

If RTS has holes instead of opaque cells then halo angular size is equal to beam angular distortion. Application of equation (1.3) is useful because undistorted part of beam does not exist. Halo is produced by the beam diffraction in the hole. Parameters р и l_g are enough for determination basic microphysical parameters.

Appendix 6.

Additional calibration coefficients are introduced in [А8]. Coefficient С₁ is indicator Fresnell approximation and it is determined as

p=C₁p_m , (a6.1)

here p is real transmission probability of RTS, p_m is measurable transmission probability of RTS. Coefficient С₁=1, if Fresnell approximation is valid.

Coefficient С₂ is indicator of a periodic arrangement of the cells in RTS. Coefficient С₂=1 if opaque cells are distributed randomly.

Appendix 7.

If layer consists of monodispers spherical particles and concentration of these particles can be changed then dependence between halo angular size and volume concentration of number of particles can be measured. For some volume concentration calibration coefficient between particle size d_c and λ/Φ_sp can be dependent from volume concentration of number of particles. This is a result of multiple scattering effects. Contribution of these effects can be measured.

CONTENT

Main Window

Discussion