Тема ТЕОРИЯ. Физика многомасштабных нелинейных процессов в атмосферах планет солнечной системы.

Научный руководитель к.ф.-м.н. А.С.Петросян

1. Разработана теория распада произвольного разрыва течений мелкой воды над уступом дна. Показана неоднозначность стационарных течений мелкой воды вблизи уступа. Проверена стационарность и автомодельность течений.

Решена задача о стационарном обтекании ступеньки потоком жидкости в приближении мелкой воды. Найдено полное решение задачи с учетом направления потока для каждой области значений глубины жидкости до ступеньки. Показано, что существует два значения глубины жидкости после ступеньки, которые соответствуют дозвуковому и сверхзвуковому течениям (неоднозначность первого типа). Из двух возможных корней уравнения физически осмысленному решению задачи ставится в соответствие одно: если поток до ступеньки сверхзвуковой, и глубина незначительно отличается от высоты ступеньки, то ступенька для него будет являться существенным препятствием, достаточным для перехода в дозвуковой режим. В этом случае реализуется дозвуковое решение справа от ступеньки. Если же поток до ступеньки сверхзвуковой, и его глубина много больше высоты ступеньки, то ступенька будет являться несущественным препятствием, оставляя поток по-прежнему сверхзвуковым и после ступеньки. Тогда выбирается сверхзвуковое решение справа от ступеньки. Таким образом, разрешается неоднозначность первого типа в случаях существенного и несущественного влияния ступеньки.. Показано, что ограничения, накладываемые условием односвязности области, занимаемой жидкостью около ступеньки, определяет характер возможных течений. Установлена связь найденных ограничений с направлением потока жидкости, и определены характеристики задачи, обусловленные отношением глубины потока к высоте ступеньки. Получены аналитические выражения для ограничений значений гидродинамических параметров течения в каждом режиме. Результаты, полученные в работе, являются неотъемлемой частью решения нестационарной задачи.

- Karelsky, K.; Petrosyan, A.; Volodkovich, A.Initial discontinuity decay problem for stationary shallow water equations on step. Geophysical Research Abstracts.EGU05-A- 08358. 2005.

- К.В. Карельский, А.С. Петросян Задача о стационарном обтекании ступеньки в приближении мелкой воды. Механика Жидкости и Газа, принята в печать(№1 2006г)

2. Разработана теория распада произвольного разрыва течений мелкой воды над уступом дна. Показана неоднозначность стационарных течений мелкой воды вблизи уступа. Проверена стационарность и автомодельность течений.

Теория основана на двухслойной модели течений жидкости с учетом особенностей процессов вблизи ступеньки. Поток разбивался на два слоя жидкости: нижний, для которого ступенька является непротекаемой границей и верхнего, для которого отсутствует прямое влияние ступеньки. Были введены необходимые дополнительные предположения об относительных скоростях формирования волновой картины в областях, определяемых различной глубиной. Такое разбиение позволило свести задачу к решению классических уравнений мелкой воды на плоскости. Предложенная модель реализует все аналитически допустимые конфигурации в случае наличия ступенчатой границы, осуществляет качественный учет диссипации поступательной механической энергии за счет турбулентности. Перечислены все возможные аналитически конфигурации в случае, когда ступенчатая граница всегда затоплена. Показаны примеры решений осуществимых моделью, но неосуществимых при аналитическом подходе.

- А.Г. Славин, К.В. Карельский, А.С. Петросян Моделирование течений невязкой тяжелой жидкости со свободной поверхностью., Труды ХLVIII научной конференции МФТИ, Современные Проблемы Фундаментальных и Прикладных Наук, ч.3, Проблемы Физики и энергетики., стр. 52-56

- А. Г. Славин Квазидвухслойная модель для потоков «мелкой воды» над ступенчатой границей., Труды Ломоносовской конференции, МГУ 2005, (принята в печать).

3. Разработан алгоритм и выполнена компьютерная реализация для моделирования пространственных гидродинамических течений над поверхностями произвольной геометрии.

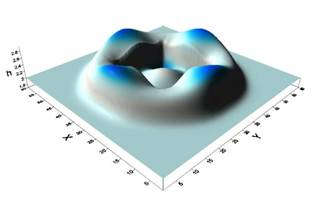
Предложена модель описания трехмерных течений жидкости над произвольной подстилающей поверхностью. В основе модели лежит аппроксимация произвольной подстилающей поверхности системой уступов и решение задачи обтекания ступенчатой границы в рамках приближений мелкой воды. Была разработана конечно-разностная схема для УМВ в двумерном случае (которая описывает реальное трехмерное течение). Представлены результаты численного расчета, основанного на предложенной модели. Как пример представлены результаты расчетов падения столба жидкости над плоской подстилающей поверхностью с углублением квадратной формы в центре расчетной области.

Рис. 1. Глубина потока жидкости t = 3 сек. после начала эксперимента.

- А.Г. Славин Модель обтекания жидкостью ступенчатой границей в приближении мелкой воды. Тезисы докладов, Конференция молодых ученых, посвященная дню космонавтики, Москва, 2005, стр.19

- Karelsky, K.; Petrosyan, A.; Slavin, A. Riemann problem for shallow water flows on step. Geophysical Research Abstracts.EGU05-A- 08202. 2005.

4. Получено кинетическое уравнение для динамики многочастичных систем при наличии испарения, конденсации и коагуляции.

Было выведено кинетическое уравнение для многочастичных систем с учётом испарения, конденсации и коагуляции, т.е. получен дополнительный член в классческом уравнении Больцмана. Полученный член был изучен при рассмотрении поведения частиц при различных условиях. А именно, получено точное решение системы при отсутствии внешних сил, рассмотрено поведение частиц при наличии произвольной силы, при наличии силы тяжести и при наличии силы Стокса. Было также получено решение для частного случая кинетического уравнения, которое достаточно хорошо согласуется с эмпирически предложенными зависимостями.

Полученные результаты дают в дальнейщем возможность понять поведение капель в присутствии турбулентных течений.

- С.В. Симакин Кинетическое уравнение испаряющихся и конденсирующих капель в облаках с учетом коагуляции. Тезисы докладов, Конференция молодых ученых, посвященная дню космонавтики, Москва, 2005, стр.18

- С.В. Симакин, К.В. Карельский, А.С. Петросян Кинетическая теория многочастичных систем при наличии испарения, конденсации и коагуляции., Труды ХLVIII научной конференции МФТИ, Современные Проблемы Фундаментальных и Прикладных Наук, ч.3, Проблемы Физики и энергетики., стр.46-52

5. Проведено исследование трехмерной сжимаемой магнитогидродинамической турбулентности методом крупных вихрей. Получены спектры магнитного поля и турбулентных флуктуаций для случая политропного газа.

Сформулирован метод крупных вихрей (LES – Large Eddy Simulation) для изучения свойств сжимаемой магнитогидродинамической (МГД) турбулентности. Получены отфильтрованные уравнения магнитогидродинамики с использованием процедуры средневзвешенной фильтрации (фильтрация по Фавру) для модели с использованием политропного соотношения между давлением и плотностью. Отфильтрованные по Фавру уравнения сжимаемой магнитной гидродинамики содержат слагаемые, описывающие подсеточные явления, для которых были предложены подсеточные параметризации: модель Смагоринского, модель Колмогорова и модель, основанная на перекрестной спиральности скорости и магнитного поля. Произведено численное моделирование отфильтрованных уравнений МГД и анализ полученных характеристик сжимаемого турбулентного течения. Полученные результаты численных расчетов различных моделей LES сравниваются с результатами прямого численного моделирования (DNS – Direct Numerical Simulation). Было показано, что предложенные в работе модели замыкания обеспечивают достаточную диссипацию кинетической и магнитной энергии, а также уменьшают численные затраты при моделировании сжимаемой магнитогидродинамической турбулентности. Было произведено сравнение трех подсеточных замыканий и выполнен анализ полученных результатов.

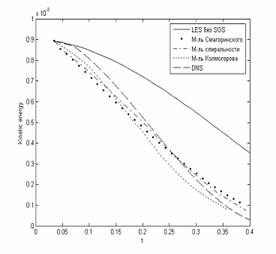
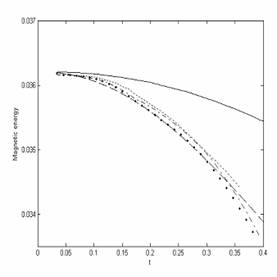
Рис.1. Временная эволюция кинетической энергии.		Рис.2. Временная эволюция магнитной энергии.

- К. В. Карельский, А. С. Петросян, А. А. Чернышов “Метод крупных вихрей для сжимаемых магнитогидродинамических течений. Фильтрация по Фавру и подсеточное моделирование” Препринт ИКИ РАН Пр-2106, 2005, 32 стр.

- А. А. Чернышов “Подсеточное моделирование в магнитогидродинамике сжимаемой жидкости” Тезисы докладов, Конференция молодых ученых, посвященная дню космонавтики, Москва, 2005, стр. 21

- Chernyshov, K. V. Karelsky, A. S. Petrosyan «Subgrid-scale modeling of large eddy simulation for compressible magnetohydrodynamic turbulence» Geophysical Research Abstracts, Vol. 7, 04385, 2005

- Chernyshov, K. V. Karelsky, A. S. Petrosyan «Subgrid-scale modeling in large-eddy simulations of compressible magnetohydrodynamic turbulence», Russian Journal of Numerical Anal. and Mathematical Modelling, (принята в печать).

6. Разработан метод крупных вихрей для исследования вырождающейся сжимаемой магнитогидродинамической турбулентности теплопроводного газа.

Разработан метод крупных вихрей для исследования сжимаемой магнитогидродинамической турбулентности с учетом уравнения для полной энергии. Теоретически выведены и обоснованы совершенно новые подсеточные слагаемые для системы уравнений МГД сжимаемой жидкости при наличии уравнения полной энергии. При рассмотрении полной системы уравнений сжимаемой МГД без предположении о политропии жидкости, резко увеличивается количество слагаемых, которые нужно параметризовать. По сравнению с гидродинамикой, в магнитогидродинамике появляются сразу несколько новых подсеточных членов, для которых были предложены подсеточные замыкания.

- А.А. Чернышов, К.В. Карельский, А.С. Петросян Исследование свойств магнитогидродинамической турбулентности методом крупных вихрей. Труды ХLVIII научной конференции МФТИ, Современные Проблемы Фундаментальных и Прикладных Наук, ч.3, Проблемы Физики и энергетики., стр.34-36

- Chernyshov, K. V. Karelsky, A. S. Petrosyan «Large-eddy simulation of magnetohydrodynamic turbulence in compressible fluid», Physics of Plasmas, (представлена в печать).

7. Создан трехмерный алгоритм и выполнена его компьютерная реализация для нахождения сжимаемых магнитогидродинамических течений, обеспечивающий второй порядок точности в областях со сложной волновой картиной, определяемой как непрерывными волновыми пакетами так и существенно нелинейными сильными разрывами.

Разработан метод сквозного счета с получением решения второго порядка точности на регулярной сетке, с откорректированными разрывными решениями, локализация которых повышена до максимально возможного для схемы Годуновского типа на регулярной неподвижной сетке. При этом метод не теряет общей устойчивости.Проведены одномерные и трехмерные тестовые расчеты, подтверждающие точность и применимость метода.

Представлены два оригинальных метода заострения разрывов в МГД течениях (с использованием реконструкции потоковых и консервативных переменных), реализованные для коррекции размытых альфеновских особенностей. Предложен простой критерий выявления размытых и требующих коррекции решений, работающий за счет отслеживания особенностей дискретного пространственного распределения типов преобладающих волн на гранях расчетных ячеек с прямыми признаками МГД разрывов.

Показано, что при адекватном использовании разработанного выше метода, на разрывных (размытых схемной вязкостью) особенностях течений, возможно корректное заострение профилей разрывов, соответствующее второму порядку точности решений в области разрывов. При этом используется устойчивый универсальный метод сквозного счета на фиксированной сетке. Так же показано, что существует предел расчетной конечнообъемной схемы на основе решения задачи Римана для максимально заостренных разрывов.

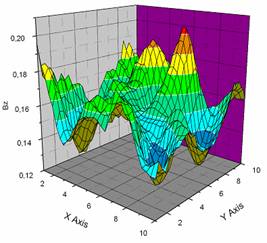
Рис.3 Результаты трехмерного моделирования взаимодействия альфвеновского разрыва со сферическим взрывом. В начальных условиях по диагонали расчетной области проходит разрыв с условиями, эквивалентными правому вращательному разрыву из одномерной тестовой задачи

- К.Н. Печерских, К.В. Карельский, А.С. Петросян Сжимаемые магнитогидродинамические течения. Численные методы высокого порядка точности., Труды ХLVIII научной конференции МФТИ, Современные Проблемы Фундаментальных и Прикладных Наук, ч.3, Проблемы Физики и энергетики., стр.43-46

- К.Н. Печерских Разрешение разрывных МГД течений методом Годунова. Тезисы докладов, Конференция молодых ученых, посвященная дню космонавтики, Москва, 2005, стр.17

- К.Н. Печерских, К.В. Карельский, А.С. Петросян Численные методы высокого порядка точности для трехмерных уравнений магнитной гидродинамики сжимаемой жидкости для сложных течений при наличии разрывов., Доклады РАН, (представлена в печать).

- Karelsky, K.; Pecherskih, K.; Petrosyan, A. Calculation method for modeling of MHD waves interactions with dusty plasma. Geophysical Research Abstracts.EGU05-A- 05082. 2005.